Курсовая работа: Работа с оптимизатором

(2)

Нам известно, что это уравнение имеет единственное решение и оно расположено на отрезке [-1; 0]. В качестве начального значения можно выбирать любую точку отрезка. Мы положим начальное значение и поместим ее в ячейку В2 на листе EXCEL, а в ячейку В3 вводим функцию и тем самым получая в этой ячейке ее значение.

В ячейку А2 введем текстовое выражение «х=», а в ячейки А1 и А3 соответственно введем следующие текстовые строки: «Начальное значение аргумента» и «Значение функции» и получим следующее окно в EXCELе:

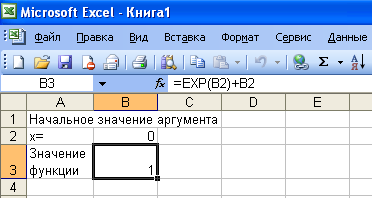
Далее выделив ячейку В3 мышкой, где хранится значение функции, используем команду «Подбор параметра» из меню «Сервис» главного меню EXCEL.

Тогда получим следующее окно на EXCELе:

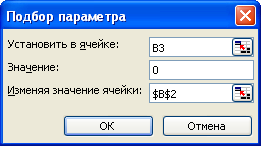
В этом окне в ячейке «Установить в ячейке» вводим адрес В3, где хранится значение функции, а в ячейку «Значение» вводим начальное значение аргумента клавиатурой равное 0 и наконец в ячейке «Изменяя значение ячейки» нажимаем мышкой а затем нажимаем на ячейке В2 т.е. введем адрес значения переменной аргумента как показано на рисунке слева.

После этого нажимаем мышкой кнопку «ОК» и получим следующее окно:

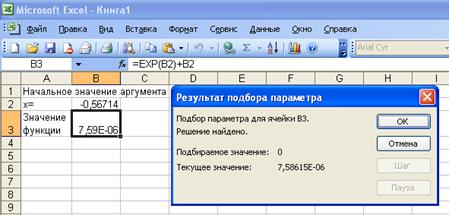
В этом окне видно, что мы получили значение аргумента в ячейке В2 = -0,56714, а в ячейке В3 округленное значение функции 7,59Е-06, а в правом окне приведено точное значение функции с 5- знаками после запятой как «Текущее значение: 7,58615Е-06.

Итак, мы получили более точное решение уравнения (2) и соответствующее ему более точное значение функции.

Численные методы решения систем линейных алгебраических уравнений на EXCEL е

При решении задач линейного моделирования требуется решить систему линейных уравнений. Рассмотрим основную задачу линейного программирования:

Min <c, x>

X Є R₁ (1)

где R ₁ = { x : Ax ≤ b , x ≥ 0 }

Задачу (1) приводим к каноническому виду: , где новые вспомогательные переменные. Здесь множество R ₁ представляет множество с угловыми точками, являющимися решениями системы уравнений:

а₁₁ х₁ + а₁₂ х₂ + … + а_{1 n} х_n + u₁ =b₁ ,

а₂₁ х₁ + а₂₂ х₂ + … + а_{2 n} х_n + u₂ =b₂ , (2)

а_{m 1} х₁ + а_{m 2} х₂ + … + а_mn х_n + u_m =b_m

Как известно, решения задач вида (1) лежат в угловых точках множества R ₁ , которых необходимо вычислить.

Из курса алгебры известно, что такие системы уравнений вида (2) мы можем решать следующими методами а) метод Крамера; б) метод Обратной матрицы; 3) метод Гаусса.

Мы рассмотрим решение систем линейных алгебраических уравнений методом Гаусса в предположении, что m=n, т.е. число уравнений и неизвестных совпадают.

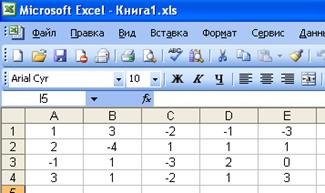
Пример 4: Решаем систему уравнений методом Гаусса:

х₁ + 3х₂ -2х₃ - х₄ =-3,

2х₁ - 4х₂ + х₃ + х₄ = 1, (2)

х₁ + х₂ - 3х₃ + 2х₄ = 0,

3х₁ + х₂ - 2х₃ + х₄ = 3