Курсовая работа: Работа с оптимизатором

y₂

…

y_i

…

y_n

Наша задача состоит в том, чтобы вычислить коэффициенты в₀ и в₁ .

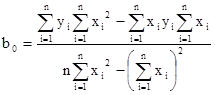, (2)

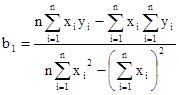, (3)

В качестве меры зависимости между случайными величинами используется коэффициент корреляции, определяемый по формуле:

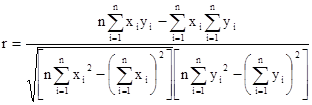(4)

Если случайные величины x и y независимы, то r = 0, если связь между y и x функциональная, то r = │1│.

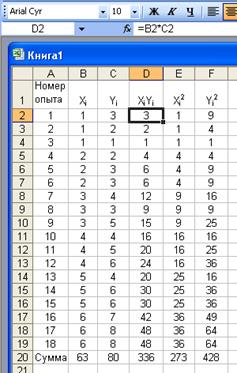
Пример. В результате эксперимента зафиксированы пары значений (x_i ,y_i ) приведенные в таблице:

x_i 1 3 2 5 2 5 6 2 3 6 4 1 3 4 6 5 1 4

y_i 3 5 3 4 3 6 7 2 3 8 6 2 4 4 8 6 1 5

Построить уравнение регрессии вида у = в₀ + в₁ х. Решение.

Для вычисления коэффициентов уравнения регрессии составляем статистическую таблицу. По вычисленным суммам определяем:

b₀ = (80*273 – 336*63)/(18*273-63² ) = 0,71;

b₁ = (18*336 – 63*80)/(18*273-63² ) = 1,07;

Тогда уравнение регрессии будет иметь вид: у = 0,71 + 1,07х.

Определяем коэффициент корреляции:

= 0,987,

Отсюда следует, что y и x тесно связаны друг с другом, т.к. коэффициент корреляции близок к единице.