Курсовая работа: Расчет информационных характеристик источников сообщений, сигналов и каналов

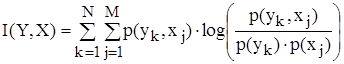
Вычисляются необходимые величины.

p(y₁ ) = p(x₁ , y₁ ) + p(x₂ , y₁ ) = 0.47 + 0.27 = 0.74

p(y₂ ) = p(x₁ , y₂ ) + p(x₂ , y₂ ) = 0.17 + 0.09 = 0.26

p(x₁ ) = p(x₁ , y₁ ) + p(x₁ , y₂ ) = 0.47 + 0.17 = 0.64

p(x₂ ) = p(x₂ , y₁ ) + p(x₂ , y₂ ) = 0.27 + 0.09 = 0.36

Все величины подставляются в формулу:

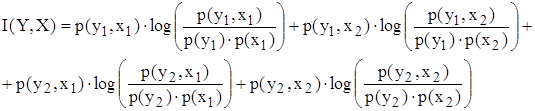
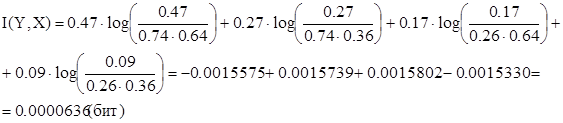
1.3 Задача № 1.84

Дискретный источник выбирает сообщения из ансамбля

.

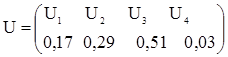Длительности сообщений соответственно равны: t_u1 =0,96 c, t_u2 =0,44 c, t_u3 =0,67 c, t_u4 =0,39 c. Определить производительность источника.

Решение:

Производительность источника рассчитывается по формуле,

где T – время, затрачиваемое в среднем на каждое сообщение при передаче, и определяемое в соответствии со следующим выражением:

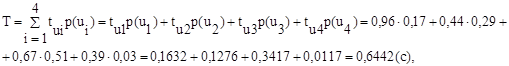
а энтропия источника H ( U ) в соответствии с формулой (1.4) [1] равна:

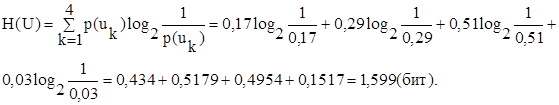
Итак, производительность источника равна:

2. Расчёт информационных характеристик дискретного канала

2.1 Задача № 2.23

На вход дискретного симметричного канала, показанного на рисунке 2, без памяти поступают двоичные символы и с априорными вероятностями p(U₁ )=0,75 и p(U₂ )=0,25.

Рисунок 2 – Дискретный симметричный канал

Переходные вероятности в таком канале задаются соотношением

,

где p=0,1 – вероятность ошибки. Определить все апостериорные вероятности .

Решение:

- переходные вероятности того, что на выходе будет символ z_j при условии, что на входе был символ u_i .