Рисунок 1 .2— Структурная схема исходной САУ

Проанализируем устойчивость САУ, используя критерий Рауса-Гурвица, суть и основные положения которого описаны в источнике [2]. Для анализа по этому критерию необходимо получить характеристический полином. Для получения характеристического полинома найдем передаточную функцию системы:

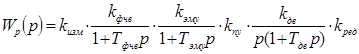, (1.4)

где — передаточная функция разомкнутой САУ.

Подставляя данные, получим:

.

Так как один из корней знаменателя нулевой, то система находится на границе устойчивости.

Теперь получим выражение для замкнутой САУ с единичной отрицательной обратной связью:

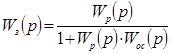, (1.5)

где — передаточная функция замкнутой САУ;

— передаточная функция обратной связи. В данном случае .

Подставив в формулу (1.5) рассчитанные ранее числовые значения, получим:

.

Получили характеристический полином 4-го порядка.

Для определения устойчивости системы запишем определитель Гурвица:

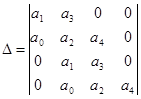, (1.6)

где — коэффициенты знаменателя соответственно.

Подставляя числа, получим:

.

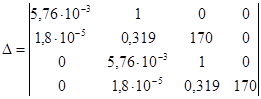Для устойчивости системы необходимо, чтобы, , , , , . Проверяем:

.

.

.

.

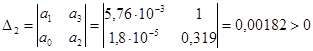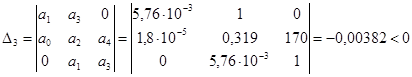Так как , то система неустойчива, а это значит, что необходимо проектировать корректирующие устройства.

2. ДИНАМИЧЕСКИЙ СИНТЕЗ САУ ПО ЗАДАННЫМ ТРЕБОВАНИЯМ К КАЧЕСТВУ ЕЕ РАБОТЫ

2.1 Определение желаемой передаточной функции

В соответствии с вариантом задания принимаем желаемую ЛАЧХ типа . Ее передаточная функция будет иметь вид:

, (2.1)

где — передаточная функция желаемой системы;

— коэффициент усиления системы;