Курсовая работа: Расчет параметров электромагнитной волны в коаксиальном кабеле марки РК-50-3-11

Основные уравнения электромагнитного поля – уравнения Максвелла. Запишем закон полного тока:

(1)

т.е. циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура L равна полному току I.

Найдем напряженность магнитного поля, продифференцируем выражение (1), получим:

(2)

Замкнутый контур L (длина окружности проводника) равен:

L=2πr, (3)

где r – расстояние от центра проводника.

Тогда уравнение примет вид:

(4)

Способность коаксиальной пары пропускать широкий спектр частот конструктивно обеспечивается коаксиальным расположением внутреннего и внешнего проводников. Особенности распространения электромагнитной энергии по коаксиальной паре обусловлено возможностью уплотнения в широком спектре частот и ставят высокочастотные связи в преимущественное положение по сравнению с низкочастотными. Взаимодействие электромагнитных полей внутреннего и внешнего проводников коаксиальной пары таково, что внешнее поле равно нулю.

Рассмотрим раздельно электрическое и магнитное поле коаксиальной пары.

Результирующее магнитное поле коаксиальной пары представлено на рис. 3, где показаны также напряженности магнитного поля Н^а _φ и Н^б _φ каждого проводника (а и б ) в отдельности. В металлической толщине проводника а магнитное поле Н^а _φ возрастает, а вне его уменьшается по закону:

Н^а _φ =I/2πr, (5)

где r‑расстояние от центра проводника.

Поле Н^б _φ проводника б изображено в соответствии с законами электродинамики, согласно которым внутри полого цилиндра магнитное поле отсутствует, а вне его выражается таким же уравнением, как и для сплошного проводника:

Н^б _φ =I/2πr, (6)

где r‑расстояние от центра полого проводника. Поэтому при определении внешних магнитных полей коаксиального кабеля параметр rдля проводников а и б принимается одинаковый и исчисляется от центра проводников (нулевой точки).

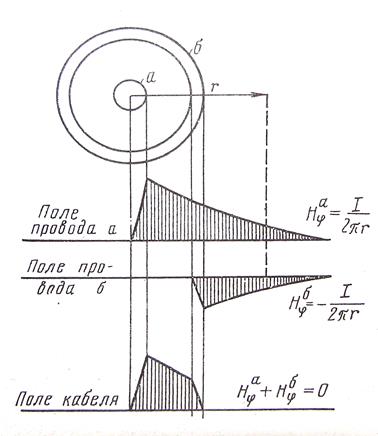
Рис. 3

Учитывая, что токи в проводниках а и б равны по величине и обратны по знаку, магнитные поля внутреннего и внешнего проводников Н^а _φ и Н^а _φ в любой точке пространства вне коаксиальной пары также будут равны по величине и направлены в разные стороны. Следовательно, результирующее магнитное поле вне коаксиальной пары по принципу суперпозиции, равно нулю:

Н_φ = Н^а _φ + Н^б _φ = I/2πr+(-I/2πr)=0. (7)

Таким образом, силовые линии магнитного поля коаксиальной пары располагаются в виде концентрических окружностей внутри нее; вне коаксиальной пары магнитное поле отсутствует. Электрическое поле будет также замыкаться внутри коаксиальной пары по радиальным направлениям между проводниками а и б , поэтому за ее пределами оно равно нулю.

На рис. 4 представлены электромагнитные поля симметричной и коаксиальной пар. Как видно, электромагнитное поле коаксиальной пары полностью замыкается внутри ее, а силовые линии электромагнитного поля симметричной пары действуют на довольно значительном от нее расстоянии. Отсутствие внешнего электромагнитного поля обусловливает основные достоинства коаксиальных кабелей: высокая защищенность от взаимных и внешних помех, малые тепловые потери в соседних цепях и оболочках, однокабельная система связи.

Рис. 4. Электромагнитное поле симметричной (а) и коаксиальной (б) цепей

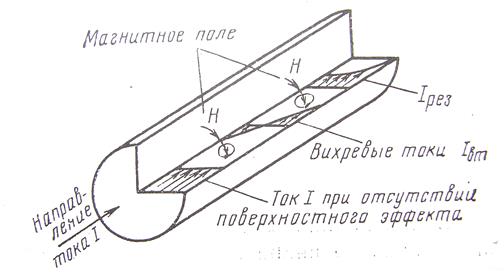
Рассмотрим действие поверхностного эффекта (скин–эффект) и эффекта близости в коаксиальных парах и определим характер распространения плотности токов в проводниках при различных частотах.

Распределение плотности тока в проводнике определяется лишь действием поверхностного эффекта (рис. 5). Силовые линии внутреннего магнитного поля, пересекая толщину проводника, наводят в ней вихревые токи, направленные согласно закону Ленца против вращения рукоятки буравчика. Как показано на рис. 5, вихревые токи I_в.т в центре проводника имеют направление, обратное движению основного тока, протекающего по проводнику, а на периферии их направления совпадают. В результате взаимодействия вихревых токов с основным происходит такое перераспределение тока по сечению проводника, при котором плотность тока возрастает к поверхности проводника. Это явление, называемое поверхностным эффектом (скин–эффектом), увеличивается с возрастанием частоты тока, магнитной проницаемости, проводимости и диаметра проводника.