Курсовая работа: Расчет профиля диффузии сурьмы в кремнии
Совершенно аналогично для междоузельных атомов:
(60)
Также находим 
:
(61)
(62)
(63)
(64)
Подставляя эти величины в выражения для концентрации заряженных дефектов, а их, в свою очередь в уравнение электронейтральности, получаем уравнение вида:
(65)
Из него мы определяем х.
Коэффициенты А, В, С и P имеют вид:
(66)
(67)
(68)
, где(69)
, (70)
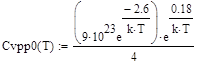, (71)
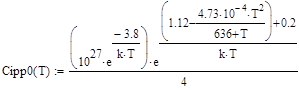, (72)
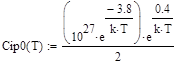, (73)
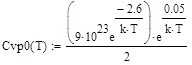, (74)
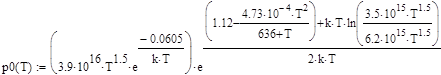, (75)
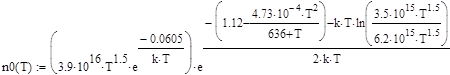, (76)
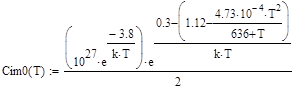, (77)
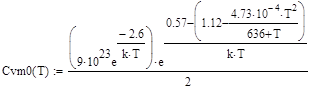, (78)
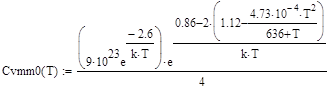. (79)
В эти выражения входят равновесные концентрации вакансий и междоузлий, которые можно определить из (25).
Температурную зависимость для ширины запрещенной зоны определяет соотношение Варшни:
.(80)
Для кремния 
, 
эВ/К, 
К [4]
|
|
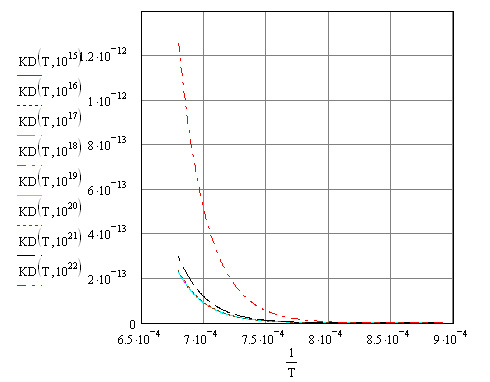
Рис. 6. Зависимость коэффициента диффузии от обратной температуры
Решая это уравнение и записывая коэффициент диффузии как
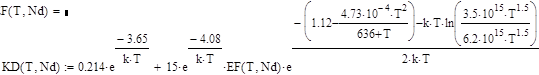(81)
где EF – решение уравнения, получаем зависимости рис. 6.
Увеличивая масштаб, получим:
|
|
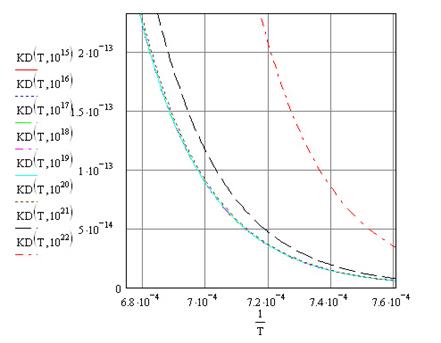
Рис. 7. Зависимость коэффициента диффузии от обратной температуры в увеличенном масштабе
|
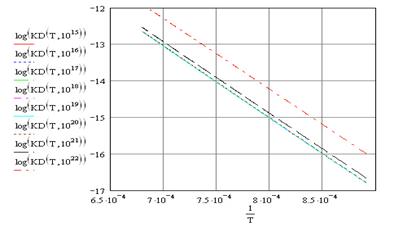
Рис. 8. Зависимость коэффициента диффузии от обратной температуры в полулогарифмическом масштабе
Зависимость в полулогарифмическом масштабе от обратной температуры приведена на рис. 8.
Увеличивая масштаб:
|
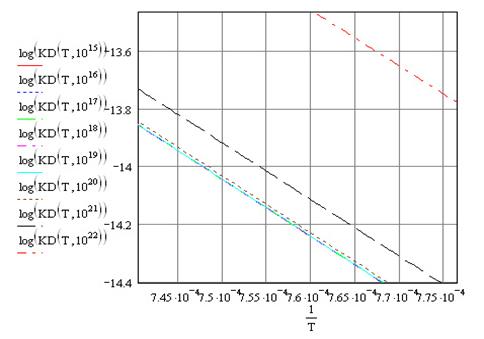
Рис. 9. Зависимость коэффициента диффузии от обратной температуры в полулогарифмическом увеличенном масштабе
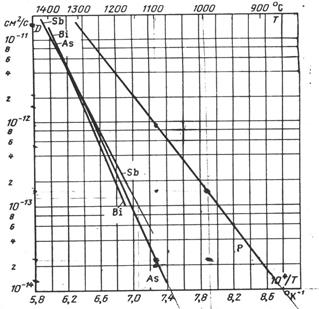
Рис. 10. Зависимость коэффициентов диффузии различных примесей в Si от обратной температуры[5]
Полученные зависимости подтверждают предполагаемую многими авторами зависимость D(T) = D0exp(-ΔE/kT).
Сравнивая данную зависимость с практическими результатами (рис. 10), например из [5], видим, что сходство теоретических и практических данных очень хорошее. Данные для сурьмы здесь приведены для максимальной поверхностной концентрации 1019 см-3 по работе [6].
Зависимость от концентрации в логарифмическом масштабе (рис. 11):
|
|
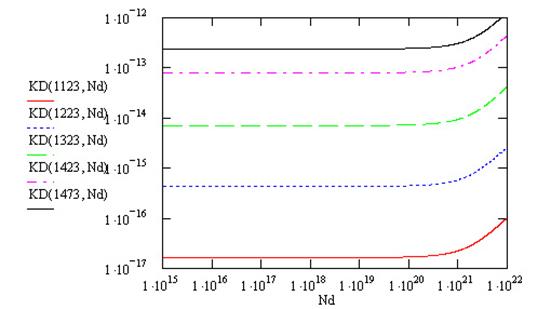
Рис. 11. Зависимость коэффициента диффузии от концентрации доноров в логарифмическом масштабе
Такое поведение графиков можно объяснить тем, что при концентрации доноров меньшей собственной концентрации, имеющей порядок 1020-1021 см-3, ее вклад практически не влияет на коэффициент диффузии. При сравнивании их по порядку, влияние начинает заметно проявляться. Когда же концентрация доноров становится большей на порядок, коэффициент диффузии начинает расти очень быстро. К слову 
.
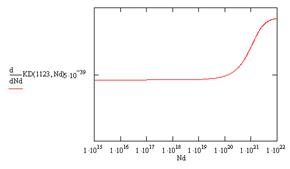
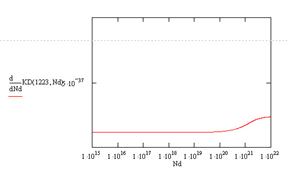
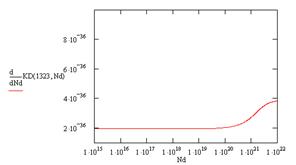
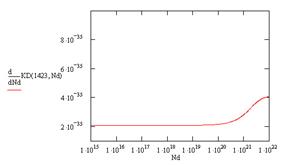
Для определения начала нелинейного участка, найдем производные коэффициента диффузии по концентрации (рис. 12).
Как видно из полученных зависимостей коэффициент диффузии не зависит от концентрации доноров до следующих значений концентрации (табл. 2).
|
|
?
|
|
?
|
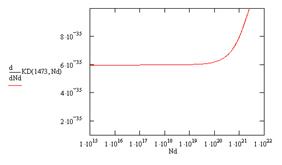
Рис. 12. Зависимость производной коэффициента диффузии от концентрации доноров при: а – 1123 К, б – 1223 К, в – 1323 К, г – 1423 К, д – 1473 К
Таблица 2. Пределы начала нелинейности в зависимости коэффициента диффузии
| Т, К | 1123 | 1223 | 1323 | 1423 | 1473 | 1573 |
| Nd, см-3 |  |  |  | | | |
Т.о., в этих диапазонах можно решать уравнение Фика в приближении отсутствия зависимости коэффициента диффузии от температуры.
Видно, что с ростом температуры поверхностная концентрация, необходимая для начала нелинейной зависимости коэффициента диффузии, немного растет. Это означает, что при более высоких температурах, коэффициент диффузии становится менее чувствительным к примеси. Это можно объяснить тем, что при повышении температуры увеличивается количество и вакансий, и междоузлий, но количество междоузлий растет быстрее, а примесь по ним перемещается медленнее.
Возможно также, что отношение созданной концентрации к собственной при более низкой температуре больше, чем при более высокой, т.е. 
, ввиду этого точка начала нелинейности смещается. Т.е. эта точка определяется собственной концентрацией при данной температуре. Это объяснение хорошо согласуется с приведенным выше, касающимся нелинейности зависимости коэффициента диффузии от концентрации доноров.
Предельная растворимость сурьмы в кремнии составляет 
см-3 при температуре 1573 К [7] и снижается до 2*1019 при 1123 К, таким образом можно утверждать, что коэффициент диффузии будет постоянен при любой концентрации доноров, то есть можно использовать решение уравнения Фика только для случая постоянного коэффициента диффузии.
Максимальная погрешность такого решения по коэффициенту диффузии составит (для 1473 К):
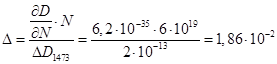,(82)
то есть все найденные решения будут удовлетворять условию, чтобы погрешность не превышала 5%. Далее покажем погрешность глубины залегания примеси, при расчете методом постоянного коэффициента диффузии.
Отметим сразу, что собственная концентрация при выбранном диапазоне температур превышает 
, в то время как максимальная предельная растворимость 
< см-3, то есть концентрация сурьмы в кремнии никогда не превысит собственную концентрацию при равновесном процессе.
Пусть диффузия ведется на глубину 10 мкм. Зададим четыре температуры процесса (1173 К, 1273 К, 1373 К и 1473 К) и сравним полученные профили концентрации в этом случае на пятом временном слое. Выбранное t составляет полчаса.