Курсовая работа: Разработка функциональной цифровой ячейки от функциональной логической схемы проектируемого узла до печатной платы узла

Рассчитываем показатель качества перестановки:

Rij = R внш it + R внш jt – R внт i – R внт j – 2 Rij, где

Rвнш it – количество связей Ei с элементами в Mt, Rbhui jt количество связей Ej с элементами в Ms, R внт i – количество связей Ei внутри модуля, R внт j – количество связей Ej внутри модуля. Выбираем ту пару, для которой показатель качества перестановки максимален.

Алгоритм:

1. Ввод начальной компоновки.

2. Расчет матриц связности Cs и Cst и заполнение их.

3. Расчет матрицы эффективности перестановок Rij для всех пар модулей.

4. Выбирается из этих матриц максимальный элемент.

5. Проверка: если показатель качества перестановок отрицательный, переход к блоку 7, иначе к блоку 6.

6. Перестановка элементов Ei и Ej и возврат к блоку 2.

7. Выход из алгоритма. Дальнейшее улучшение с помощью данного
алгоритма невозможно [3].

Таким образом, 18 логических элементов размещаются в 6 микросхемах (по 3 элемента в каждой) оптимальным образом. Для этого используем программу PROG (18 элементов, 6 блоков максимальные значения входных данных для компоновки). Алгоритм работы в этой программе:

1) В соответствии со своей принципиальной электрической схемой заполняют симметричную матрицу смежности. В этой матрице у нас будет 18 строк и 18 столбцов, что соответствует количеству логических элементов. Последовательно перебирая все элементы, ищут номера повторяющихся цепей. На пересечении i-той строки и j-ro столбца ставят цифру (от 1 до 4), которая и означает количество связей, одинаковых цепей i-ro элемента с j-тым. Главная диагональ такой матрицы – нули. Заполнив матрицу, смотрят предварительную схему соединений (F2). В ней 64 внешних связей и 7 внутренних. Таким образом, на данном этапе используют последовательный алгоритм предварительной компоновки, предварительное разрезание (быстрое получение результата) в автоматическом режиме. Полученная матрица представлена ниже:

Таблица 1

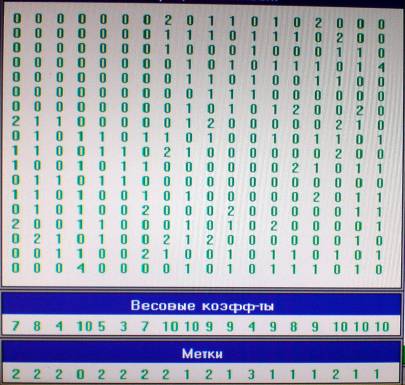
Где весовой коэффициент – числовой коэффициент, параметр, отражающий значимость, относительную важность, «вес» данного фактора, показателя в сравнении с другими факторами, оказывающими влияние на изучаемый процесс.

Весовые коэффициенты равны количеству связей конкретного элемента с остальными элементами схемы.

Обозначение элементов метками:

1. Выбирается элемент с имеющий максимальную локальную степень (чей весовой коэффициент максимален) – элемент №4. Для данного элемента устанавливается метка М = 0.

2. Выбираются элементы, связанные с элементом с М = 0. Данные элементы помечаются меткой М = 1. Элементы №9, 11, 13, 14, 15, 17, 18

3. Выбираются элементы, связанные с элементами с М = 1 и не имеющими меток. Данные элементы помечаются меткой М = 2. Элементы 1, 2, 3, 5, 6, 7, 8, 10, 16.

4. Выбираются элементы, связанные с элементами с М = 2 и не имеющими меток. Данные элементы помечаются меткой М = 3. Элемент 12.

На этом этап обозначение элементов метками закончен. Далее идет первоначальная компоновка элементов.

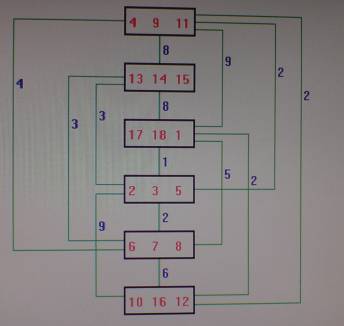Рис. 2. Предварительная схема соединений

Применение этого алгоритма приводит к постепенному ослаблению внутриблочных связей от первого блока до последнего.

2) Работают с матрицами Ро. Их 15 штук (фактически, это схема соединений в матричном виде). Выбираем из матриц ту, у которой максимальное значение элемента матрицы (4,3 и т.д.). В ней меняют местами компоненты, пересечение которых и дает этот элемент матрицы. Смотрят промежуточный результат компоновки: видно, что количество внутренних связей увеличивается по сравнению с первоначальным числом (клавиша F2 для просмотра схемы соединений), а количество внешних связей уменьшается. Затем снова выбирают матрицу с максимальным значением элемента. Продолжать до тех пор, пока все элементы всех матриц не станут отрицательными, либо равными нулю. На данном этапе улучшают начальную компоновку итерационным алгоритмом. То есть основная идея этого алгоритма и этого этапа заключается в межблочных перестановках пар элементов с целью минимизации общего количества межблочных связей. Итоговый вид всех матриц Итоговый вид всех матриц:

Рис. 3. Итоговый вид всех матриц

0 итераций (нет перестановок). Внешних связей: 64, внутренних связей: 7.

1 итерация (1-ая перестановка). Внешних связей: 59, внутренних связей: 12.

2 итерация (2-ая перестановка). Внешних связей: 54, внутренних связей: 17.

3 итерация (3-я перестановка). Внешних связей: 49, внутренних связей: 22.