Курсовая работа: Разработка функциональной цифровой ячейки от функциональной логической схемы проектируемого узла до печатной платы узла

11 блок – выполняется эквивалентное преобразование матрицы с целью увеличения количества нулей. Если в блоке 5 свободных нулей не найдено, то надо их добавить – для этого в незанятых строках, не помеченных «+» находится минимальный элемент, больший нуля hmin. Вычитаем hmin из элементов всех строк, не помеченными «+» и прибавляем ко всем элементам строк столбцов, помеченных «+».

Исходными данными для работы алгоритма является матрица эффективности назначений, для ее вычисления мы должны построить матрицы R и D (связей и расстояний соответственно) и получить все элементы матрицы эффективности назначений по формуле:

Cij = ri, 1di, 1 + ri, 2di, 2 + … + ri, j-1di, j-1 + ri, jdi, j, где i, j – номера строки и столбца, на пересечении которых находится элемент. В нашем случае программа сама рассчитывает матрицу эффективности назначений. Исходными данными для нее служит матрица, отражающая координаты выводов микросхем и разъема.

Первоначальное подключение цепей к контактам разъема

Первоначальное подключение берется из задания, также вычисляется суммарная оценка длины проводников, определяющая качество данного назначения выводов разъема.

№ вывода разъема	№ проводника, подключаемого к разъему
1	4
2	8
3	12
4	20
5	16
6	24
7	28
8	2
9	27
10	15
11	7
12	17

Оценка длины проводника подключаемого к разъему – длина цепи, включающей все выводы элементов и вывод разъема с одинаковыми номерами.

Пример расчета оценки длины проводника для 1 вывода разъема.

1. Исходя из эскиза печатной платы (см Приложение 2) находятся координаты выводов подключенных к 1-му выводу разъема и координаты самого вывода разъема. Разъем: (97,5; 50), вывод 1 (0; 0) вывод 2 (12,5; 0)

2. Аналитически находится оптимальная последовательность подключения выводов к разъему. Последовательность: вывод 1 – вывод 2 – разъем.

3. Расчет оценки длины проводника

4. Аналогично рассчитываются остальные оценки длин.

Такое подключение, возможно, не является оптимальным, для оптимизации первоначального подключения цепей к разъему применяются алгоритмы линейного назначения. В данной курсовой работе используется программа, основанная на венгерском алгоритме. Для получения матрицы назначений в программе требуется заполнить следующую таблицу (см рис 6).

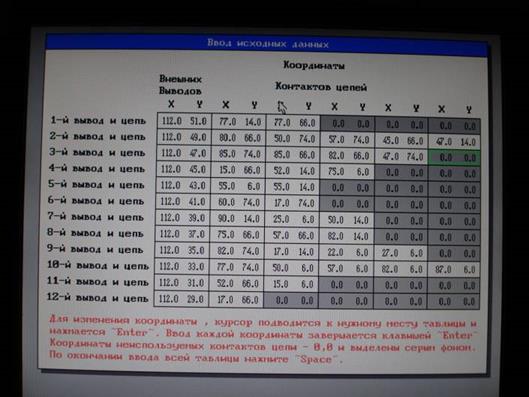
Рис. 10. Исходные данные программы оптимизации подключения цепей к разъему

Алгоритм заполнения таблицы.

1. Согласно имеющимся данным по микросхеме К155ЛА4 (Рис. 11 и Рис. 12) и данным по компоновке логических элементов в блоки составляется соответствие выводов каждого блока и вывода корпуса.

2. Согласно данным по размещению (Раздел 2) составляется эскиз печатной платы с размещенными на ней корпусами микросхемы (см Приложение 2). Выбирается произвольная точка, которая служит началом координат

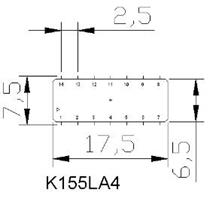Рис. 11. Корпус микросхемы	Рис. 12. Соответствие логических выводов микросхемы выводам корпуса

5. Согласно полученному эскизу печатной платы каждому выводу корпуса назначается своя координата относительно начала координат.

Рис. 13 Матрица D до начала выполнения алгоритма венгра

Рис. 13 Матрица D после выполнения алгоритма венгра

Результат выполнения программы – более оптимальное подключение цепей к контактам разъема.

№ вывода разъема	№Вывода разъема после переназначения
1	17
2	7
3	27
4	24
5	12
6	8
7	15
8	2
9	28
10	16
11	20
12	4

Проведем проверку длин цепи до и после переназначения вывода разъема.

Рассмотрим цепь №17

До переназначения выводов: L=95+38=133 мм

После переназначения выводов: L=95+12=107 мм

Суммарная длина проводников уменьшилась, следовательно, найдено более оптимальное назначение выводов разъема.

5. Трассировка электрических соединений контактов элементов