Курсовая работа: Разработка функциональной цифровой ячейки от функциональной логической схемы проектируемого узла до печатной платы узла
5 итерация (5-ая перестановка). Внешних связей: 45, внутренних связей: 26.
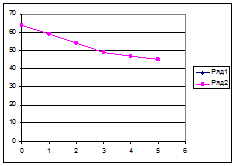
Рис. 4. График зависимости числа внешних связей от числа итераций
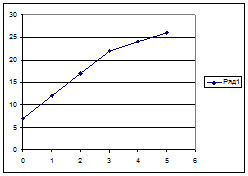
Рис. 5. График зависимости числа внутренних связей от числа итераций
3) После работы с матрицами на экран выводится схема соединений. Это и есть оптимальное расположение (компоновка) элементов в конструкции (элементов в микросхемах и микросхем между собой).

Рис. 6. Схема соединений
Видно, что процесс оптимизации связан с увеличением внутренних связей и уменьшением внешних. После каждой перестановки число внутренних связей увеличивается, а число внешних – уменьшается. Это связано с тем, что меняются местами элементы из разных микросхем, которые являются компонентами матриц Ро. В результате задача оптимизация будет выполнена: в заданное количество блоков (микросхем) расположили с минимальным количеством внешних связей между ними по 3 элемента. Это облегчит дальнейшие этапы моделирования.
4) Осталось скомпоновать разъем с микросхемами, так как у него тоже есть электрические связи с элементами и он является частью конструкции. Фактически, повторяется п. 1 нашего алгоритма, но без заполнения матрицы смежности, так как программа не предусматривает компоновку с количеством блоков, равным 7. Для каждой микросхемы, начиная с первой, смотрят номера цепей элементов в ней, которые повторяются с номерами цепей этого разъема. На схеме соединений ставится связь от разъема к микросхеме с цифрой, которая говорит о числе совпадений цепей разъема и микросхемы. Повторять то же самое для оставшихся 5 микросхем. Соответственно, получаем схему соединений, которая будет представлять взвешенный граф с 7-ю элементами: 6 микросхем и 1 разъем. Изменяются и графики зависимостей, так как разъем увеличивает число внешних связей (в данном случае на 46).
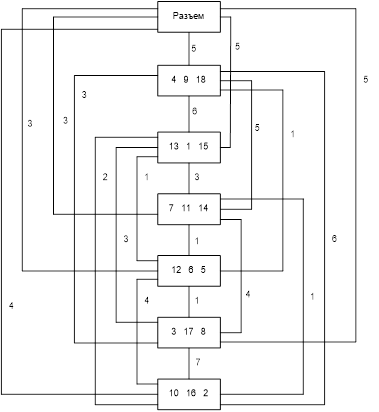
Рис. 7. Схема соединений с учетом разъема
 |
| Рис. 8. График зависимости числа внешних связей от числа итераций внешних связей от числа итераций с учетом разъема. |
3. Размещение элементов на коммутационных платах
Постановка задачи размещения.
Дано:
E = {e1, e2, e3, e4, e5, e6, e7} – множество элементов схемы устройства.
P = {p1, p2, p3, p4, p5, p6, p7} – множество установочных позиций на коммутационной плате для размещения элементов.
Задача размещения состоит в определение соответствия между элементами устройства и установочными позициями печатной платы. Разъем (элемент е7) может находиться только в одной конкретной позиции (позиция p7), все остальные элементы однотипны, а позиции равноправны, следовательно мы имеем 6! Вариантов размещений элементов на плате. Такая задача называется задачей дискретного размещения. Для того чтобы упростить задачу размещения и не перебирать все 6! вариантов решений используются различные комбинационные методы. В данной курсовой работе используется метод ветвей и границ.
Метод ветвей и границ.
Ход решения.
Соответствие блоков полученных в разделе 1 элементам.
| Блок | Элемент |
| 4, 9, 18 | e1 |
| 13, 1, 15 | e2 |
| 7, 11, 14 | e3 |
| 12, 6, 5 | e4 |
| 3, 17, 8 | e |
| 10, 16, 2 | e6 |
| Разъем | e7 |
1. Определение последовательности элементов.
Последовательность элементов строится исходя из оптимизированной компоновки (рис 4.), по ней определятся количество между элементами. Элемент, наиболее связанный с разъемом: е2.
Дальнейшая последовательность элементов (каждый элемент наиболее связан с предыдущими): е1, е3, е5, е6, е4.
2. Составление матрицы D и матрицы S.
Матрицы составляются исходя из оптимизированной компоновки (рис 7.).
| Матрица S | Матрица D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3. Расчет верхней границы – функции качества размещения.
Функция качества размещения рассчитывается следующим образом:
1. Разъем (е7) помещается в позицию (р7). Все остальные элементы остаются неразмещенными.