Курсовая работа: Разработка функциональной цифровой ячейки от функциональной логической схемы проектируемого узла до печатной платы узла
Нижняя оценка рассчитывается следующим образом:
F = Fн + Fнр + Fр, где:
1. Fн – оценка длины связи между не размещенными элементами
2. Fнр – оценка длины связи между не размещенными и размещенными элементами
3. Fр – значение длины связи между размещенными элементами
Для расчета нижних оценок используется программа placeing.
Минимальная нижняя оценка при размещение в позицию p6 = 4560. Элемент закрепляется в позиции p6.
3. Аналогично пункту 2 выбираются элемент наиболее связанный с размещенными элементами и разъемом. Перебираются возможные варианты размещение элемента и выбирается такое размещение, нижняя оценка которого минимальна. Элемент закрепляется в данной позиции.
4. Пункт 3 выполняется до тех пор, пока не будут размещены все элементы. Полученное размещение:
| Позиция | Элемент |
| p1 | e4 |
| p2 | e6 |
| p3 | e5 |
| p4 | e3 |
| p5 | e1 |
| p6 | e2 |
| p7 | Разъем |
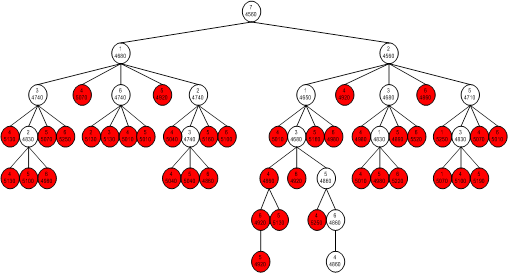
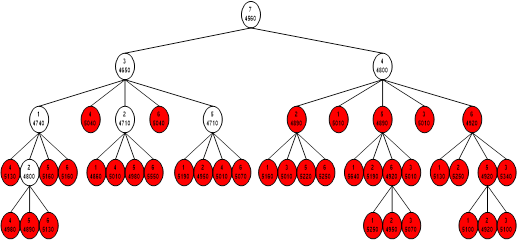
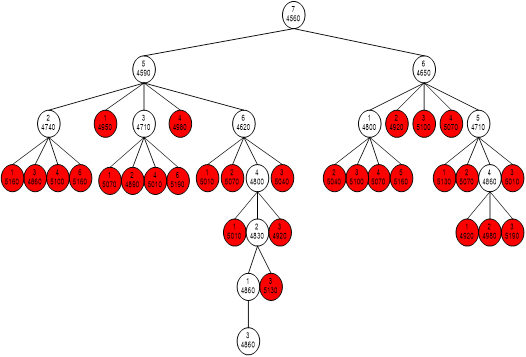
4. Дальнейшее исследование возможных вариантов размещения.
Во время исследования отсекаются бесперспективные варианты решения (те варианты, у которых нижняя оценка больше верхней границы).
Приведем полученное дерево:
4. Минимизация длины связей между контактами разъема и контактами внешних цепей
На данном этапе необходимо используя Венгерский алгоритм минимизировать длины связей между контактами разъёма и контактами внешних цепей.
Назначение осуществляется в полуавтоматическом режиме с помощью «Венгерского алгоритма» (с использованием программы VENGR.EXE).Структурная схема «венгерского алгоритма» показана на рисунке 7.
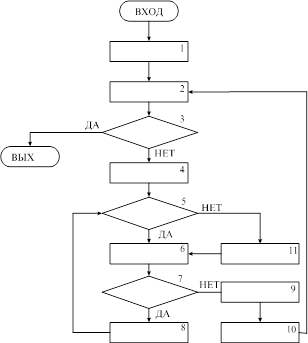
Рисунок 9 – структурная схема венгерского алгоритма.
1 блок – начальное преобразование матрицы эффективности в эквивалентную матрицу. Для этого из каждой строки вычитается минимальный элемент.
2 блок – в полученной матрице эффективности помечаются нули, образующие правильное решение, таким образом, чтобы в каждой строке и столбце было не более одного помеченного нуля.
3 блок – проверка: получен ли полный правильный выбор нулей. Выбор нулей называется полным, если помечено нулей, где – размерность матрицы. Если получен полный правильный выбор, то – к выходу, если «нет», то к блоку 4.
4 блок – помечаем «+» столбцы, в которых есть нули со «*». Таким образом помечаем все ребра, инцидентные вершинам. Каждый «+» соответствует вершине.
5 блок – проверка: есть ли в матрице незанятые нули. Нуль называется незанятым, если его строка и его столбец не помечены «+».
6 блок – помечаем незанятый нуль «/».
7 блок – проверка: есть ли в строке нуля, помеченного «/» в блоке 6 нуль со «*», если «да», то переход в блок 8.
8 блок – если в строке есть нуль со «*», то снимаем «+» со столбца, в котором он находился, а строку помечаем «+».
9 блок – если нуля со «» в строке нет, то это означает, что можно увеличить количество нулей со «*» на 1. Строится расширяющая цепочка, начиная с последнего помеченного нуля (блок 6): переходим по столбцу к нулю со «», по строке к нулю со «/», по столбцу к нулю со «*», пока цепочка не прервется. Возможно, что цепочка прервется сразу.