Это – стандартные (типовые) показатели качества, они понятны для заказчиков. Оказывается, что все четыре показателя теснейшим образом связаны с запасами устойчивости по амплитуде и по фазе. Поэтому, обеспечение стандартных показателей качества обеспечивает необходимую устойчивость.

Исследуем заданный объект на устойчивость, найдём передаточную функцию разомкнутой системы.

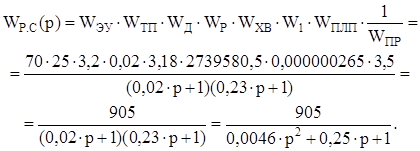
Набираем передаточную функцию на ЭВМ в пакете MatLab 7.1, при помощи команды step(W), получаем график переходного процесса (рисунок 4.1).

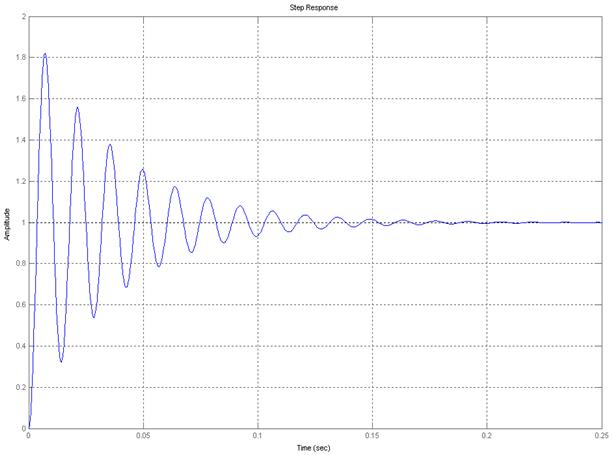
Рисунок 4.1 – Переходный процесс системы

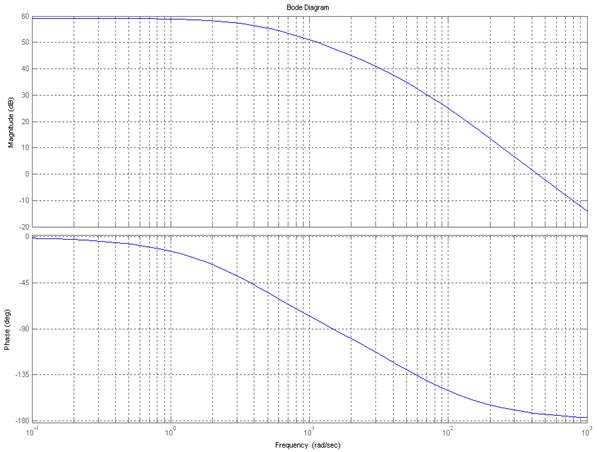
Рисунок 4.2 – ЛАХ и ЛФХ системы

ЭВМ выдает график переходного процесса, из графика видно, что система при исходных данных устойчива, но не удовлетворяет требуемым показателям качества (M ≤ 3).

Передаточная функция ошибки по управляющему воздействию:

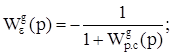
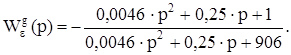
Коэффициенты ошибок найдем по передаточной функции ошибки управления путем деления числителя передаточной функции на знаменатель, т.о. получили:

С0 = 0,001104;

С1 = 0,000276;

С2 = 0,000005.

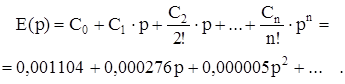
Для того чтобы добиться заданных показателей качества (tp = 2 с; коэффициент перерегулирования ) вводим корректирующее устройство.

Применим последовательное корректирующее устройство. Передаточная функция разомкнутой скорректированной системы равна исходной, умноженной на передаточную функцию корректора:

[WP(p)]Ж = WP(p)Н · WP(p)КУ.

Корректирующее устройство включено последовательно в контуре системы в любом месте. Для исследования идеально подходят ЛАЧХ (так как они складываются при последовательном соединении). Задаются желаемые ЛАХ и ЛФХ и тогда:

LЖ(w) = LН(w) + LКУ(w);

φЖ(w) = φН(w) + φКУ(w);

5 СИНТЕЗ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

Получили, что передаточная функция системы имеет вид:

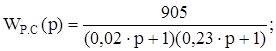
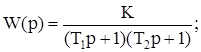
T1 = 0,02 c;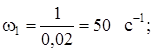

T2 = 0,23 c;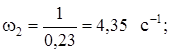

К = 905; 20∙lg(K) = 59,13.

По полученным данным строим неизменяемую ЛАХ (НЛАХ) (рисунок 5.2).

По номограмме Солодовникова (рисунок 5.1) определяем диапазон частоты среза в зависимости от заданного времени регулирования и величине перерегулирования . Вычислим частоту среза.

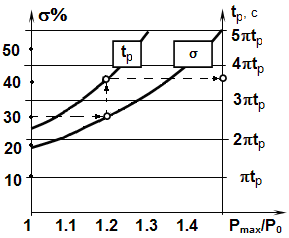
Рисунок 5.1 – Номограмма Солодовникова

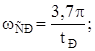
Желаемая ЛАХ определяется показателями качества и точностью процесса регулирования. Среднечастотная часть желаемой ЛАХ характеризуется частотой среза. Частота среза определяется с помощью номограммы Солодовникова. Для наиболее простой реализации корректирующего устройства последовательные изломы наклонов высокочастотной желаемой ЛАХ и ЛАХ неизменяемой части системы должны совпадать.