Курсовая работа: Разработка схемы блока арифметико-логического устройства для умножения двух двоичных чисел

Разрабатываемое АЛУ будет иметь восьмиразрядный вход данных X, восьмиразрядный вход данных Y, шестнадцатиразрядный выход результата Z, вход начала вычисления START, выход готовности результата READY, вход принудительного сброса R и тактовый вход C (рис.2.1).

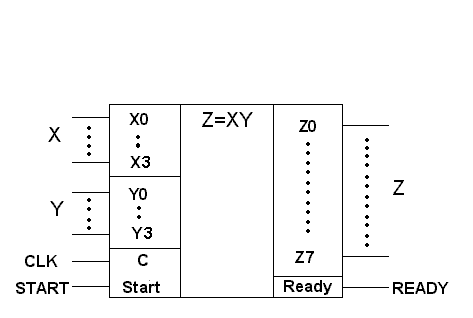
Рисунок 2.1 Условное графическое изображение АЛУ.

При разработке структурной схемы необходимо обратить внимание на уменьшение количества применяемых элементов , что в свою очередь приведет к снижению потребляемой мощности. Одновременно с этим необходимо обеспечить время вычисления менее заданного. Также необходимо уделить внимание предотвращению гонок в схеме.

Исходными данными для разработки структурной схемы является алгоритм вычисления. В соответствии с заданным алгоритмом вычисления для его реализации как минимум потребуются два регистра для хранения и сдвига операндов. Для реализации счётчика потребуется три триггера. Для определения окончания вычисления необходима схема сравнения J с 0.

Для реализации математических вычислений потребуется восьмиразрядный сумматор.

Разработанная структурная схема показана на рис. 2.2. В этой схеме множитель Y и результат Z хранятся в одном сдвиговом 16-ти разрядном регистре RgY. Регистры RgХ и RgY имеют как прямые, так и инверсные выходы , что позволяет уменьшить количество элементов в сумматоре.

Рисунок 2.2 Структурная схема АЛУ для умножения двоичных чисел.

Как видно из схемы активный уровень сигналов управления - высокий, и устройство управления тактируется по фронту импульса, а исполнительные устройства - по спаду, что позволяет избежать гонок в схеме.

3 Синтез Компонентов

3.1 Синтез сумматора

Так как построить сумматор сразу для восьми разрядов достаточно сложно, сумматор будем выполнять по схеме последовательного соединения полных одноразрядных сумматоров.

Таблица истинности полного двоичного сумматора приведена в табл.3.1, где а и b - слагаемые, S - сумма, P - перенос из предыдущего разряда. Рn – перенос в следующий разряд.

Таблица 3.1

а	B	P	S	Рn
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

По таблице истинности строим карты Карно (рис.3.1) и проводим минимизацию логических выражений, описывающих работу полного сумматора.

S Pn

	0	1	0	1		0	0	1	0
P	1	0	1	0	P	0	1	1	1
a

Рисунок 3.1 Карты Карно для полного сумматора.

(3.1)

(3.2)

Полученные выражения (3.1) и (3.2) приводим к заданной элементной базе:

(3.3)

(3.4)

По полученным выражениям строим схему полного сумматора (рис.3.2).

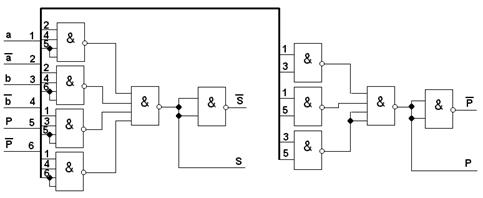
Рисунок 3.2 Принципиальная схема полного сумматора.

Нулевой разряд сумматора для экономии элементов построим по схеме полусумматора. Таблица истинности полусумматора представлена в табл.3.2.

Таблица 3.2

А	B	S	Ро
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

По таблице истинности получаем логические выражения: