Курсовая работа: Разработка цифрового электропривода продольной подачи токарно-винторезного станка

, (1.16)

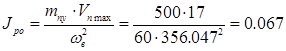(кг×м² ); (1.17)

(кг×м² ). (1.18)

Таким образом, динамический момент сопротивления:

(Н∙м) (1.19)

Максимальный динамический момент, который может обеспечить двигатель, равен:

(Н×м). (1.20)

(102.621 < 470).

В статическом и динамическом режиме двигатель обеспечивает необходимый момент для преодоления сил сопротивления, следовательно, выбор сделан правильно.

1.2 Расчет основных параметров системы управления

Одной из основных характеристик системы управления является период дискретности . Для систем с астатизмом первого порядка период дискретности определяется допустимой величиной скоростной ошибки и допускаемым ускорением :

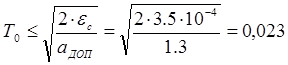(с). (1.21)

Однако расчет по этой формуле гарантирует соблюдение лишь одного условия – траектория ускоренного движения рабочего органа за время не отклонится от заданной траектории больше, чем на величину .

Следует учесть, что при проектировании привода необходимо обеспечить устойчивость и требуемую полосу частотного диапазона. Эти параметры зависят от периода дискретности , величина которого определяет форму частотной характеристики в высокочастотном диапазоне. Поэтому необходимо сначала построить желаемую частотную характеристику системы, а затем определить период дискретности.

На рисунке 1.2 изображена желаемая логарифмическая амплитудно-частотная характеристика (ЛАЧХ), форма которой позволяет:

· устранить позиционную ошибку – первая асимптота имеет наклон к оси частот 20 дБ/дек;

· ограничить скоростную ошибку – первая асимптота должна занять определенное положение на оси относительной амплитуды ;

· обеспечить устойчивую работу привода – ЛАЧХ имеет асимптоту, которая пересекает ось частот с наклоном 20 дБ/дек;

· обеспечить требуемый частотный диапазон привода и показатель колебательности – должна быть обеспечена необходимая длина асимтоты в частотном диапазоне .

Рисунок 1.2 – желаемая форма ЛАЧХ цифрового электропривода

Желаемая ЛАЧХ описывается следующей дискретной частотной характеристики (ДЧХ):

, (1.22)

где ; ; ; – основные параметры, определяемые требованиями к системе электропривода;

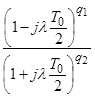– характеристика запаздывания, определяемая параметрами цифровой системы.

Для определения основных параметров ДЧХ необходимо преобразовать заданные параметры технологического процесса в эквивалентные параметры гармонического сигнала, которые позволяют определить положение критической точки запретной области ЛАЧХ.

Преобразования параметров возможны в тех случаях, когда движения рабочих органов задаются в виде круговых траекторий. При развертке во времени одной из координат круговой траектории движения получим синусоиду:

, (1.23)

поверхности; – угловая скорость (подача).

Первая и вторая производные (скорость и ускорение) гармонического сигнала определяются известными выражениями:

(1.24)