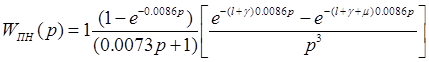Курсовая работа: Разработка цифрового электропривода продольной подачи токарно-винторезного станка

Дискретная передаточная функция неизменяемой части представляется Z-преобразованием:

(3.2)

где – z-преобразование передаточной функции приведенной неизменяемой части; .

Неизменяемая часть включает в себя экстраполятор, формирователь тока якоря, двигатель постоянного тока и датчик обратной связи, которые описываются передаточными функциями – , , , соответственно.

Передаточная функция формирователя тока описывает соединение двух звеньев, включенных последовательно и образующих единую систему – преобразователь (ТП или ШИП) и якорную цепь двигателя. В результате такого объединения исключается математическое описание преобразователя, который имеет сложную форму выходного напряжения, и математический анализ производится относительно импульсов тока якоря, форма которых проще. При этом передаточная функция формирователя тока приобретает следующий вид:

, (3.3)

где – коэффициент передачи по току;

– относительная длительность импульса напряжения (<1);

– целое число периодов дискретности , на которое запаздывает импульс напряжения относительно времени подачи управляющего сигнала, принимаем l=1 (для ШИП);

– дробная часть периода дискретности (0<<1), характеризующая величину запаздывания импульса напряжения;

– функция запаздывания;

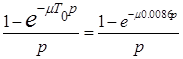– функция длительности импульса напряжения.

– постоянная времени якорной цепи двигателя.

Постоянная времени цепи якоря , определяется по формуле:

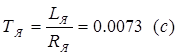, (3.4)

где – суммарные значения индуктивностей и сопротивлений обмотки якоря электродвигателя, трансформатора, уравнительных реакторов и дросселя, соединительных проводов и силовой цепи преобразователя.

Учитывая, что передаточная функция якорной цепи введена в передаточную функцию формирователя тока, в структуре двигателя (рисунок 3.2) остается лишь звено, описывающее электромеханическую часть двигателя:

. где . (3.5)

Рисунок 3.2 – Структурная схема двигателя постоянного тока

В качестве датчиков скорости применяются устройства, инерционность которых неизмеримо мала по сравнению с периодом дискретности. Поэтому они могут быть представлены пропорциональным звеном с передаточной функцией:

. (3.6)

С учетом изложенного передаточная функция приведенной неизменяемой части приобретает вид:

(3.7)

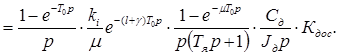(3.8)

Произведя преобразования, получим:

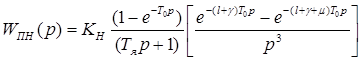, (3.9)

где 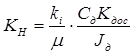– коэффициент передачи неизменяемой части.