Курсовая работа: Разработка цифрового электропривода продольной подачи токарно-винторезного станка
Отсюда можно определить эквивалентные параметры гармонического воздействия – частоту и амплитуду:
, 
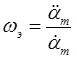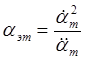. (1.25)
Максимальная ошибка для дискретной системы определяется выражением:
, (1.26)
где 
– дискретная частотная характеристика системы, 
– псевдочастота.
Для низкочастотного участка ЛАЧХ справедливо допущение 
. Тогда:
. (1.27)
Если известно значение ошибки 
, то должно быть выполнено условие:
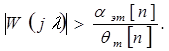
(1.28)
Для относительной амплитуды 
это условие запишется в следующем виде:
(1.29)
В системах управления электроприводами значения максимальной скорости 
, допускаемого ускорения 
и допускаемой скоростной ошибки 
известны.
Тогда, учитывая условия преобразования, для обеспечения необходимой точности желаемая ЛАЧХ должна проходить выше критической точки 
с координатами:
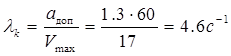; (1.30)
. (1.31)
44.932 дБ
При этом запретная область ограничивается по относительной амплитуде первой асимптотой, которая проводится влево от точки с наклоном -20 дБ/дек. По частоте эта запретная область ограничивается второй асимптотой, которая проводится вправо от точки с наклоном -40 дБ/дек. Положение запретной зоны показано на рисунке 1.3.
Рисунок 1.3 – Построение запретной зоны по критериям точности
Скоростная ошибка 
определяет необходимую добротность системы по скорости 
, которая определяется по формуле:
, (1.32)
Значение соответствует точке пересечения линии, которая продолжает первую низкочастотную асимптоту, с осью 
.
После построения запретной области строятся логарифмические амплитудные и фазовые частотные характеристики. При построении следует придерживаться следующего порядка.
1. Первая низкочастотная асимптота желаемой ЛАХ проводится с наклоном –20 дБ/дек выше точки 
на 3 дБ, чтобы обеспечить запас устойчивости. Подъем характеристики приводит к увеличению коэффициента добротности по скорости в 
раза:
. (1.33)
2. Вторая асимптота проводится с наклоном –40 дБ/дек от точки сопряжения с координатами (
; 
) до точки пересечения с осью , которая определяет базовую частоту 
запретной области:
. (1.34)
3. По заданному показателю колебательности 
определяется частота сопряжения второй и третьей асимптот:
. (1.35)