Курсовая работа: Решение дифференциальных уравнений. Обзор

При решении задачи с шагом h=0.1 назовем шаг h2, аргумент - x2, а решение - y2.

Определим начальное условие

Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator

Определим шаг формулы Эйлера - шаг интегрирования

Определим по формулам Эйлера значения приближенного решения в узлах сетки

Выведем в рабочий документ вычисленные значения решения. Для сравнения рядом выведены значения решения, вычисленные с большим шагом

Построим график решения y2(x2)

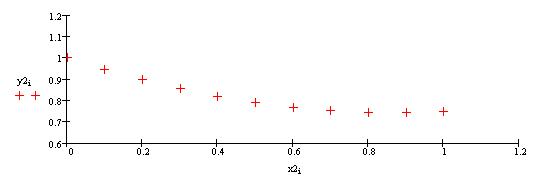
Построим на одном графике оба приближенные решения

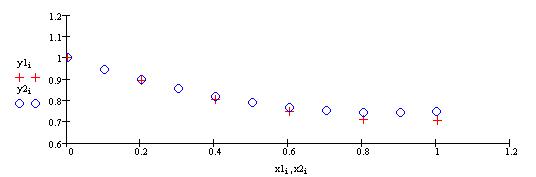
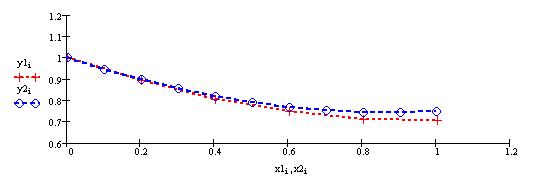
Для того чтобы одновременно построить графики нескольких функций от разных аргументов, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции у оси абсцисс имя первого аргумента, запятую, имя второго аргумента, и т.д., разделяя имена аргументов запятой.

Аналогично, в позиции возле оси ординат введите имя функции первого аргумента, запятую, имя функции второго аргумента и т.д.разделяя имена функций запятой.

Когда функции определены, щелкните по рабочему документу вне поля графиков.

2.3 Метод Рунге – Кутты

Методом Рунге-Кутты четвертого порядкаточности называют одношаговый метод, относящийся к широкому классу методов Рунге-Кутты. В этом методе величиныy_i+ 1 вычисляются по следующим формулам:

y_i +1 =y_i +h(k₁ + 2k₂ + 2k₃ +k₄ )/6 , i= 0, 1, ...

k₁ =f(x_i ,y_i ),