Курсовая работа: Решение дифференциальных уравнений. Обзор

k₃ =f(x_i +h/2,y_i +hk₂ /2),

k₄ =f(x_i +h,y_i +hk₃ ).

Найдем на [0, 1]приближенноерешение задачи Кошиy' = sinx– cosy,y(0)=1методом Рунге-Кутты 4-го порядка с шагом h=0.2 и методом Эйлера с тем же шагом.Изобразим оба приближенные решения графически

Для решения задачиметодом Рунге-Кутты воспользуемся функциейrkfixed

Определим начальное условие - решение в начальной точке

Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator

Определим правую часть уравнения

Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.

Вычислим приближенное решение на отрезке [0,1], выполнив n=1/h=5 одинаковых шагов, методом Рунге-Кутты 4-го порядка; обозначим приближенное решение Y

Выведем в рабочий документ вычисленное приближенное решение

Для того чтобы вывести значение переменной в рабочий документ, введите имя переменной, знак равенства и щелкните по рабочему документу вне выделяюшей рамки

В первом столбце приведены значения x, во втором столбце - соответствующие значения приближенного решения

Решим ту же задачу методом Эйлера

Выведем в рабочий документ вычисленное приближенное решение, и, для сравнения, решение, вычисленное методом Рунге-Кутты

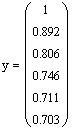
Построим графики приближенных решений