Курсовая работа: Решение краевых задач в среде виртуальной гибридной машины

150, -12

Чтобы получить конечно-разностную модель дифференциального уравнения, необходимо сначала интервал или область решения разделить с постоянным шагом по осям координат на требуемое число подинтервалов и для каждой внутренней точки подставить аппроксимирующие выражения в заданное уравнение. После приведения подобных членов в каждом уравнении, получится система алгебраических уравнений при полной дискретизации всех независимых переменных или система дифференциальных уравнений - при неполной дискретизации. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области.

В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Поэтому аппроксимирующие, выражения производных из таблиц 1-4 для точек у левой границы интервала берутся из верхних строчек, а для точек у правой границы - из нижних строчек.

2. КРАЕВАЯ ЗАДАЧА В ЧАСТНЫХ ПРОИЗВОДНЫХ

В качестве демонстрационной краевой нестационарной задачи возьмем задачу теплопроводности с непрерывным временем. На этой задаче удобно показывать как динамику нагрева объекта, так и установившееся распределение температурного поля.

2.1 Задача теплопроводности с непрерывным временем

Применение метода прямых рассмотрим на примере решения уравнения теплопроводности следующего вида:

,

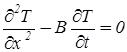которое описывает изменение температуры вдоль металлического стержня длиной в 1 метр (), вваренного своими концами в две металлические пластины с разными, постоянно поддерживаемыми на них температурами

и .

Начальное распределение температуры по длине будем задавать для внутренних точек как

.

Единичную длину стержня разобьем на 8 равных частей

()

и обозначим изменяющееся значение температуры в каждой точке через .

2.2 Вариант аппроксимации дифференциальными уравнениями

Применим трех точечную аппроксимацию частной производной второго порядка, воспользовавшись таблицей 2 из раздела 1.4. Для внутренних точек и для приграничных точек коэффициенты в аппроксимирующем выражении второй производной оказываются одинаковыми. Это позволяет для каждой внутренней точки, размеченного на 8 частей стержня, записать следующую систему дифференциальных уравнений первого порядка относительно скорости изменения температур в каждой точке:

Для получения числовых значений зададим конкретные величины. Так коэффициент В для теплоизолированного по боковой поверхности алюминиевого стержня равен теплопроводности этого материала, т.е. l=200 вт/(м×К).

Удвоенный квадрат шага по длине стержня равен 2´0.125² =0.03125 м² .

Вместо температуры введем относительную переменную, разделив левую и правую части на 100°:

.

Если все коэффициенты перенести в правую часть и, вычислить, записав результат перед скобками, то система уравнений примет окончательный вид:

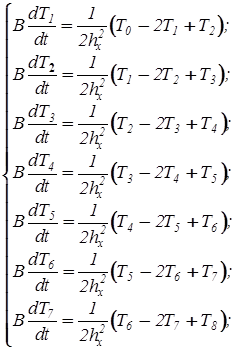
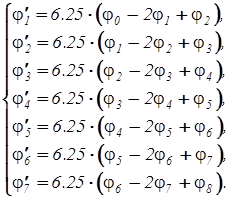
В полученной системе j ₀ =1, а j ₈ =0.

В случае аппроксимации производной по времени конечными разностями «вперед», что в цифровой моделирующей среде может случиться и при непрерывном времени, соотношение между шагом по временной переменной и по пространственной должно подчиняться следующему неравенству: 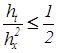. При несоблюдении этого условия решение может оказаться численно неустойчивым.

2.3 Программирование для математического моделирования

Полученная в пункте 2.2 система дифференциальных уравнений, благодаря представлению искомых переменных в относительном виде, при максимальных напряжениях на выходах операционных блоков в 1 вольт и масштабных множителях, равных единице, специального расчета коэффициентов передач не требует. Коэффициенты по входам сумматоров будут такими же, как в уравнениях.

????? ?????????? ???????????? ?????? ??? ???? ?????? ???????? ?? ??????? 1.

Рисунок 1