Курсовая работа: Симметpия относительно окpужности

Достаточно заметить, что эти треугольники имеют общий угол, а из равенства |OA|·|OA¢| = R² = |OB|·|OB¢| следует равенство отношений |OA|/|OB¢| = |OB|/|OA¢|. Обратите внимание, что в отличие от подобия, пропорциональность связывает стороны [OA] и [OB¢], [OB] и [OA¢], а не [OA] и [OA¢], [OB] и [OB¢]. Из подобия получаем ÐOBA = ÐOA¢B¢.

V.

|A¢B¢| = |AB|

|OA|·|OB|·R² .

Действительно, по свойству IV имеем

|A¢B¢| = |AB|·|OA¢|

|OB|= |AB|

|OA|·|OB|·R² .

VI. Прямая a, проходящая через центр инверсии, отображается в себя. Если же O Ï a и A - основание перпендикуляра из точки O на прямую a (рис. 4), то образом прямой a будет окружность w₁ , построенная на отрезке [OA¢] как на диаметре (A¢ = inv_O ^R (A)).

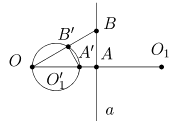
Рис. 4

Для доказательства этого свойства рассмотрим произвольную точку B прямой a. По свойству IV ÐOB¢A¢ = ÐOAB = 90^° . Следовательно точка B¢ лежит на окружности с диаметром [OA¢]. Удивление от такого неожиданного действия инверсии на произвольную прямую пройдет, если принять в расчет бесконечно удаленную точку. Каждая прямая проходит через ¥. Поэтому переход ¥ в точку O заставляет концы прямой сжиматься к точке O. Следующее свойство позволяет определить центр окружности, которая является образом прямой из свойства VI.

VII. Пусть w₁ = inv_O ^R (a). Обозначим через O₁ = S_a (O), где S_a - осевая симметрия с осью a (рис. 4). Тогда центром окружности w₁ является точка O₁ ¢ = inv_O ^R (O₁ ).

Сохраняя принятые в предыдущем свойстве обозначения, имеем |OO₁ | = 2|OA|. Подставляя это в равенство |OA|·|OA¢| = R² = |OO₁ |·|OO₁ ¢| получаем |OO₁ ¢| = |OA¢|/2. Поэтому точка O₁ ¢ является серединой отрезка [OA¢].

VIII. Окружность w₁ (O₁ ,r), проходящая через центр инверсии, отображается на некоторую прямую a. Более того, если A - конец диаметра, проходящего через O и O₁ (A ¹ O), то прямая a проходит через точку A¢ = inv_O ^R (A) и перпендикулярна прямой (OO₁ ).

Справедливость этого свойства сразу следует из свойств III и VI.

IX. Окружность w₁ (O₁ ,r₁ ), не проходящая через центр инверсии, отображается при inv_O ^R на некоторую окружность w₂ (O₂ ,r₂ ). Точнее, если точки A и B являются концами диаметра, лежащего на прямой (OO₁ ) (рис. 5), то отрезок [A¢B¢] является диаметром окружности w₂ (A¢ = inv_O ^R (A), B¢ = inv_O ^R (B)).

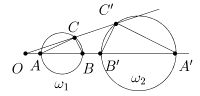
Рис. 5

Для доказательства рассмотрим произвольную точку C окружности w₁ и покажем, что C¢ = inv_O ^R (C) Îw₂ . Из свойства IV имеем равенства ÐOCA = ÐOA¢C¢ и ÐOCB = ÐOB¢C¢. Поэтому ÐA¢C¢B¢ = ÐOB¢C¢- ÐOA¢C¢ = ÐOCB-ÐOCA = 90^° . Следовательно C¢Îw₂ .

Переходит ли центр O₁ в центр образа w₂ , точку O₂ ? Никогда (убедитесь в этом с помощью прямых вычислений, т.е. докажите, что O₁ ¢ = inv_O ^R (O₁ ) не может быть серединой [A¢B¢]). Этот "недостаток" инверсии с лихвой компенсируется замечательным ее свойством сохранять величину угла. Напомним, что угол между пересекающимися окружностями по определению равен углу между касательными к этим окружностям в точке их пересечения. Аналогично определяется и угол между пересекающимися прямой и окружностью. Рассмотрим частный случай: для двух касающихся окружностей w₁ и w₂ определим величину угла между inv_O ^R (w₁ ) и inv_O ^R (w₂ ). Вид образов inv_O ^R (w₁ ) и inv_O ^R (w₂ ) во многом зависит от положения точки O относительно окружностей w₁ и w₂ . Так, если O Ïw₁ Èw₂ , то из свойств I и IX получаем, что inv_O ^R (w₁ ) и inv_O ^R (w₂ ) являются касающимися окружностями. Если же O лежит только на одной из окружностей, например на w₁ , то из свойств I, VIII и IX получим касающиеся прямую inv_O ^R (w₁ ) и окружность inv_O ^R (w₂ ). И, наконец, если O совпадает с точкой касания окружностей, то inv_O ^R (w₁ ) и inv_O ^R (w₂ ) являются параллельными прямыми (величина угла между параллельными прямыми по определению равна нулю). Итак, в каждом из случаев, величина угла между inv_O ^R (w₁ ) и inv_O ^R (w₂ ) равна нулю. Аналогично можно установить, что если прямые a и b параллельны, то величина угла между inv_O ^R (a) и inv_O ^R (b) также равна нулю.

X. Инверсия сохраняет величину угла между прямыми, пересекающимися окружностями, пересекающимися прямой и окружностью.

Докажем сначала, что для любых прямых угол Ða,b совпадает с углом между inv_O ^R (a) и inv_O ^R (b). Утверждение очевидно, если прямые проходят через точку O. Пусть теперь O Î a и O Ï b (рис. 6). Обозначим через w₁ окружность, в которую переходит прямая b, и через b₁ - касательную к w₁ в точке O. Так прямые b и b₁ перпендикулярны одному и тому же диаметру, то они параллельны. Поэтому угол между a и w₁ , равный по определению углу между a и b₁ , совпадает с углом Ða,b. Рассуждения аналогичны и в случае, когда O Ï aÈb (надо рассмотреть касательные к окружностям inv_O ^R (a) и inv_O ^R (b) в точке O).

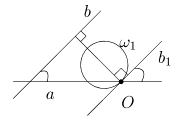
Рис. 6

Поскольку угол между окружностями и между прямой и окружностью определялся через касательные, то доказательство остальных двух утверждений легко сводятся к случаю сохранения угла между прямыми.

Основой решения целого ряда геометрических проблем является удачное применение того или иного преобразования плоскости. При этом мы считаем использование какого-либо преобразования удачным, если образы рассматриваемых фигур поддаются простому геометрическому анализу. В задаче Фаньяно¹ , например, стороны треугольника наименьшего периметра получаются из отрезка прямой серией осевых симметрий. При отыскании точки Ферма² похожая идея реализуется с помощью поворота на 60^° . В следующих параграфах попробуем выяснить насколько способность к упрощению свойственна инверсии. Этот параграф закончим решением проблемы A.

Решение A. Обозначим через A, B, C, и D соответственно точки касания w₁ Çw₂ , w₂ Çw₃ , w₃ Çw₄ и w₄ Çw₁ . Сделаем инверсию с центром в O = A относительно окружности некоторого радиуса R. По свойству VIII и IX получим пару параллельных прямых a = inv_O ^R (w₁ ), b = inv_O ^R (w₂ ) и пару касающихся окружностей w₃ ¢ = inv_O ^R (w₃ ) и w₄ ¢ = inv_O ^R (w₄ ) (рис. 7).