Курсовая работа: Симметpия относительно окpужности

|B¢C¢|:|A¢D¢|

|B¢D¢|= |AC|/(|OA|·|OC|)

|BC|/|OB|·|OC|:|AD|/(|OA|·|OD|)

|BD|/(|OB|·|OD|)=

= |AC|

|BC|:|AD|

|BD|.

Следующая теорема является решением проблемы H.

Теорема. Пусть даны точки A, B и число k > 0 (k ¹ 1). Множество F состоит из всех таких точек X плоскости, для которых |XA|:|XB| = k. Тогда F является окружностью (окружность Аполлония), центр которой лежит на прямой (AB).

Доказательство. На прямой (AB) можно легко найти две точки O и C, принадлежащие множеству F (одна из них будет внутренней точкой отрезка [AB], другая - внешней точкой этого отрезка). Рассмотрим инверсию относительно окружности с центром в точке O произвольного радиуса R. Для образов точек A, B и C имеем

|C¢A¢|

|C¢B¢|= |CA|R² /(|OC|·|OA|)

|CB|R² /(|OC|·|OB|)= |CA|

|CB|:|OA|

|OB|= k:k = 1. 1

Пусть X¢ = inv_O ^R (X) и F¢ = inv_O ^R (F). Тогда, учитывая (1) и сохранение при инверсии отношения четырех точек, получаем

X ÎFÛ|XA|

|XB|:|CA|

|CB|= k:k = 1Û

Û|X¢A¢|

|X¢B¢|:|C¢A¢|

|C¢B¢|= 1Û|X¢A¢|

|X¢B¢|= 1.

Последнее означает, что F¢ - серединный перпендикуляр к отрезку [A¢B¢]. Отсюда F = inv_O ^R (F¢) - окружность, диаметр которой лежит на прямой (AB).

Формула следующей теоремы, названная в честь Леонарда Эйлера⁶ , связывает между собой радиусы вписанной и описанной окружностей произвольного треугольника с расстоянием между их центрами.

Теорема. Пусть для произвольного треугольника ABC числа r, R и d соответственно обозначают радиусы вписанной и описанной окружностей и расстояние между их центрами. Тогда d² = R² -2Rr.

Доказательство. Точки касания вписанной окружности w(O,r) со сторонами [AB], [AC] и [BC] обозначим соответственно через K, L и M (рис. 11).

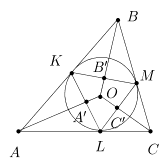
Рис. 11