Курсовая работа: Симметpия относительно окpужности

6) Следует из 1) и 2) и из подобия треугольников DKO₁ C и DLCO_a .

Лемма доказана.

Лемма 2. Для окружностей w(O,R) и w₁ (O₁ ,R₁ ) условие inv_O ^R (w₁ ) = w₁ выполнено тогда и только тогда, когда w^w₁ .

Доказательство. Пусть inv_O ^R (w₁ ) = w₁ , wÇw₁ = {A,B} и w₁ Ç(OO₁ ) = {X,Y}. Тогда inv_O ^R (X) = Y. Отсюда |OX|·|OY| = R² = |OA|² . Поэтому (OA) - касательная к окружности w₁ . Что означает (OA)^(O₁ A) и w^w₁ .

Предположим теперь, что w^w₁ . Обозначим через w₂ = inv_O ^R (w₁ ). Из свойства X получаем w₂ ^w. Поскольку существует единственная окружность, проходящая через A и B (по-прежнему, {A,B} = wÇw₁ ) и перпендикулярная w, w₂ = w₁ . Лемма доказана.

Теорема (Фейербах). Окружность Эйлера треугольника ABC касается вписанной и трех вневписанных окружностей этого треугольника.

Доказательство. Сохраним некоторые обозначения леммы 1. Середины сторон треугольника обозначим через A¢, B¢ и C¢ (рис. 14). На отрезке [XX_a ] как на диаметре построим окружность w. Из леммы 1 сразу получаем, что точка A¢ будет центром w (так как |BX| = |CX_a |), а ее радиус R = |XX_a |/2 = (a-2|BX|)/2 = (b-c)/2 (далее предполагаем, что b ³ c). Рассмотрим симметрию относительно w. Из условий w₁ ^w и w₁ ^w и из леммы 2 заключаем, что inv_O ^R (w₁ ) = w₁ и inv_O ^R (w_a ) = w_a . Чтобы найти образ окружности Эйлера (w_э ) при инверсии относительно w введем дополнительные обозначения.

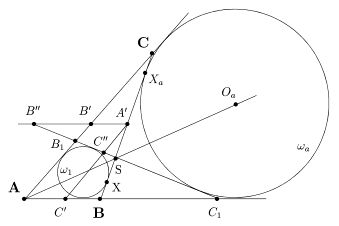
Рис. 14

Пусть S - общая точка биссектрисы [AO_a ) и прямых (BC) и (B₁ C₁ ). Тогда |SC| = ab/(b+c) и |SB| = ac/(b+c). Отсюда

|SA¢| = (|SC|-|SB|)/2 = a

2·b-c

b+c.

Пусть также точки B¢¢ и C¢¢ являются соответственно пересечением касательной (B₁ C₁ ) с прямыми (A¢B¢) и (A¢C¢). Из подобия треугольников DSA¢B¢¢ и DSBC₁ получаем

|A¢B¢¢| = |BC₁ |·|SA¢|

|SB|= (b-c)·a

2·b-c

b+c

a·c

b+c

= (b-c)²

2c.

Поскольку |A¢B¢| = c/2,

|A¢B¢|·|A¢B¢¢| = (b-c)² /4 = R² . (1)

Рассматривая подобные треугольники DA¢SC¢¢ и DCSB₁ приходим к

|A¢C¢¢| = |B₁ C|·|SA¢|

|SC|= (b-c)·a

2·b-c

b+c