a_{М 1} x₁ + a_{М 2} x₂ + ... + a_{М N} Х_N = b_М

Так как Z - линейная функция, то Z = С_j , (j = 1, 2, ..., n), то все коэффициенты линейной функции не могут быть равны нулю, следовательно, внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть на границе области, но исследовать точки границы невозможно, поскольку частные производные являются константами.

Для решения задач линейного программирования потребовалось создание специальных методов. Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные.

Цель данной курсовой работы: изучить и научиться применять на практике симплекс - метод для решения задач линейного программирования.

Задачи курсовой заботы:

1. привести теоретический материал;

2. на примерах рассмотреть симплекс метод;

3. представить данную курсовую работу в виде презентации.

Математическое программирование

Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи математического программирования формулируются следующим образом: найти экстремум некоторой функции многих переменных f ( x₁ , x₂ , ... , x_n ) при ограничениях g_i ( x₁ , x₂ , ... , x_n ) * b_i , где g_i - функция, описывающая ограничения, * - один из следующих знаков £, =, ³, а b_i - действительное число, i = 1, ... , m. f называется целевой функцией.

Линейное программирование – это раздел математического программирования, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями, которым должны удовлетворять искомые переменные.

Задачу линейного программирования можно сформулировать так. Найти max

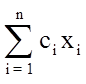
при условии: a₁₁ x₁ + a₁₂ x₂ + . . . + a_1n x_n £ b₁ ;

a₂₁ x₁ + a₂₂ x₂ + . . . + a_2n x_n £ b₂ ;

. . . . . . . . . . . . . . . . . . . . . . . . . . .

a_m1 x₁ + a_m2 x₂ + . . . + a_mn x_n £ b_m ;

x₁ ³ 0, x₂ ³ 0, . . . , x_n ³ 0 .

Эти ограничения называются условиями не отрицательности. Если все ограничения заданы в виде строгих равенств, то данная форма называется канонической.

В матричной форме задачу линейного программирования записывают следующим образом.

Найти:

max c_T x

при условии:

A x £ b;

x ³ 0 ,

где А - матрица ограничений размером (m´n),

b(m´1) - вектор-столбец свободных членов,

x(n ´ 1) - вектор переменных,

с_Т = (c₁ , c₂ , ... , c_n ) - вектор-строка коэффициентов целевой функции.

Решение х₀ называется оптимальным, если для него выполняется условие: