Курсовая работа: Симплекс метод в форме презентации

Симплекс-метод реализует упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки, осуществляются последовательные переходы от одной допустимой экстремальной точки к другой, пока не будет найдена точка оптимального решения.

Обозначим: N– общее количество переменных в ЗЛП, представленной в канонической форме; n- количество исходных переменных; m - количество ограничений, n_q - количество дополнительных переменных, тогда N=n+n_q . Каждая вершина многогранника решений имеет m - ненулевых переменных и

(N-m) - нулевых переменных. Ненулевые переменные называются базисными, нулевые переменные – небазисными. Дополним систему равенств равенством целевой функции, при этом будем считать, что z является m+1 базисной переменной, которая всегда присутствует в базисе для любой вершины.

Для получения решения составляется начальный допустимый базис, в котором базисные переменные должны быть представлены в виде единичных орт. Это означает, что уравнения, представляющие данную вершину должны включать каждую базисную переменную только в одной строке с коэффициентом, равным 1.

При выборе начального допустимого базиса для составления симплекс-таблицы на первом шаге исходные x₁ ,x₂ переменные приравниваются к нулю и являются небазисными, среди введённых дополнительных переменных выбираются переменные с коэффициентами равными единице. Переменные x₃ ,x₄ ,x₅ в равенствах (2) - (4) являются базисными и в z - строку входят с коэффициентами, равными 0. Для заполнения симплекс-таблицы необходимо целевую функцию преобразовать к виду

.

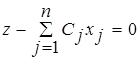Таким образом, окончательно получаем:

(1)

(2)

(3)

(4)

При составлении симплекс-таблицы придерживаются следующих правил:

1. в крайнем левом столбце располагаются базисные переменные и z;

2. в крайнем правом столбце располагаются правые части ограничений;

3. в первой строке располагаются переменные в определённом порядке: сначала z, потом небазисные переменные, базисные переменные располагаются в последних m столбцах перед правой частью.

св.	z	x1	x2	x3	x4	x5
z	0	1	-C1	-C2	0	0	0
X3	b1	0	a11	a12	1	0	0
X4	b2	0	a21	a22	0	1	0
X5	b3	0	a31	a32	0	0	1

Идею рассмотрим на примере:

7x₁ +5x₂ →max

2x₁ +3x₂ ≤19

2x₁ +x₂ ≤13

3x₂ ≤15

3x₁ ≤18

x₁ ≥0, x₂ ≥0

Запишем задачу в каноническом виде. При необходимости предварительно неравенство преобразовать так чтобы все свободные члены были неотрицательными.

Симплекс метод в последовательном преобразовании системы уравнений до получения нужного решения. В общем случае те переменные, в системе уравнений, определитель при которых не равен 0 и является максимумом порядка, называются базисными переменными.

7x₁ +5x₂ →max

2x₁ +3x₂ +x₃ =19

2x₁ +x₂ +x₄ =13

3x₂ +x₅ =15

3x₁ +x₆ =18