,

Ограничения:

1. Правые части всех ограничений должны быть неотрицательными b_i ≥0, i=1,..m. Если какой-нибудь из коэффициентов b_i < 0, то необходимо коэффициенты ограничения слева и справа домножить на "-1" и изменить знак данного ограничения на противоположный;

2. Все ограничения должны быть представлены в виде равенств, поэтому при переходе от неравенства к равенству используют аппарат дополнительных переменных. Если исходные ограничения определяют расход некоторого ресурса (знак ""), то переменные x_j ≥0, j=n+1,…kследует интерпретировать как остаток, или неиспользованную часть ресурса. В этом случае x_j – остаточная переменная и вводится в уравнение со знаком "+". Если исходные ограничения определяют избыток некоторого ресурса (знак ""), то вводится избыточная переменная x_j ≥0, j=k+1,…Nзнаком "-".

Переменные:

· Все переменные должны быть неотрицательными, т.е. x_j ≥0, j=1,…n.

· Если переменная не имеет ограничения в знаке, то её нужно представить как разность двух неотрицательных переменных: x=x^’ -x^’’ , где x^’ ≥0, x^’’ ≥0. Такую подстановку следует использовать во всех ограничениях, содержащих эту переменную, а также в выражении для целевой функции. Если такая переменная попадает в оптимальное решение, то

.

Целевая функция:

· Подлежит максимизации или минимизации. maxz= - min(-z)

· Система ограничений в виде равенств и неравенств образует выпуклое множество - выпуклый многогранник. Это множество может быть ограниченным и неограниченным. Целевая функция задачи линейного программирования также является выпуклой функцией. Таким образом, задача линейного программирования является частным случаем задачи выпуклого программирования.

Рассмотрим систему ограничений задачи линейного программирования в виде равенств

(1)

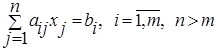
· Система (1) линейных уравнений совместна, если она имеет, по крайней мере, одно решение.

· Система (1) называется избыточной, если одно из уравнений можно выразить в виде линейной комбинации остальных.

· В системе (1) число переменных (неизвестных x_j ) n больше, чем число ограничений m. Будем считать, что ранг этой системы равен m (система не избыточна) и что система (1) совместна. Тогда m переменных из общего их числа образуют базисные переменные, а остальные (n-m) переменных называют небазисными.

· Если система уравнений имеет решение, то она имеет и базисное решение.

· Решение системы уравнений (1) называют допустимым, если все его компоненты неотрицательны.

· Если система линейных уравнений обладает допустимым решением, то она имеет и базисное допустимое решение. Совокупность всех допустимых решений системы (1) есть выпуклое множество, т.е. множество решений задачи линейного программирования выпукло. Так как это множество образовано плоскостями (гиперплоскостями), то оно имеет вид выпуклого многогранника. Базисное допустимое решение соответствует крайней точке выпуклого многогранника (его грани или вершине). Если существует оптимальное решение задачи линейного программирования, то существует базисное оптимальное решение.

Целевая функция задачи линейного программирования есть уравнение плоскости (или гиперплоскости для числа переменных больше трех). Максимальное или минимальное значение целевая функция задачи линейного программирования достигает либо в вершине выпуклого многогранника, либо на одной из его граней. Таким образом, решение (решения) задачи линейного программирования лежит в вершинах выпуклого многогранника и для его нахождения надо вычислить значения целевой функции в вершинах выпуклого многогранника, определяемого условиями – ограничениями задачи.

Решение задачи линейного программирования симплекс-методом

Прямая задача.

Рассмотрим задачу линейного программирования в канонической форме:

Найти максимум (минимум) функции

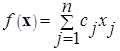
при условиях

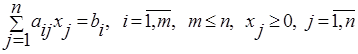
Предполагается, что решение этой задачи существует. Чтобы найти оптимальное решение, надо найти допустимые базисные решения, а из них выбрать оптимальное базисное решение.

Симплекс – метод – это алгебраический метод решения задач линейного программирования. В процессе вычислений производиться последовательный обход вершин многогранника решений (ОДР) с проверкой в каждой вершине условий оптимальности. При этом каждый переход в смежную вершину сопровождается улучшением целевой функции.

Вычислительные процедуры симплекс – метода