Курсовая работа: Синтез и анализ машинного агрегата
В результате построения плана скоростей определяются:
VD = (pd) ∙ kV = 55 ∙ 0,04 = 2,20 м/c;
VDC = (cd) kV = 16,5 ∙ 0,04 = 0,66 м/c.
Скорость точки S 4 определяется по принадлежности звену 4 аналогично определению скорости точки S 2 по теореме подобия…
Звено 5 совершает поступательное движение, поэтому скорости всех точек звена одинаковы и равны скорости точки D .
Величина угловой скорости звена 4 определяется аналогично предыдущему:
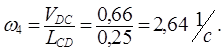
Для определения направления ω4 отрезок cd плана скоростей устанавливается в точку D , а точка С закрепляется неподвижно; тогда становится очевидным, что ω4 направлена по часовой стрелке.
1.5.2 Построение плана ускорений
Механизм I класса (звено 1).
Точка А кривошипа 1 совершает вращательное движение вокруг О1 , поэтому её ускорение есть сумма нормального и тангенциального ускорения:
Поскольку принято n 1 = const (следовательно ε1 = 0 ), то
Модуль ускорения
На плане скоростей этот вектор изображается отрезком πа = 158 мм,
направленным от А к О1 . Тогда масштаб плана ускорений
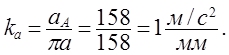
Группа Ассура II 1 (2,3).
Внешними точками группы являются точки А и О3 , внутренней – точка В . Составляется система векторных уравнений, связывающих ускорение внутренней точки с ускорениями внешних точек:
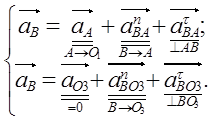
В этой системе модули нормальных ускорений
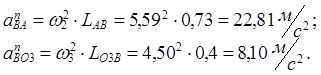
На плане ускорений векторы 
и 
изображаются отрезками
an`= 
В результате построения плана ускорений определяются модули ускорений:
AB = (πb) ∙ ka = 127 ∙ 1 = 127 м/c
;
∙ka = 26 ∙ 1 = 26 м/c;
= (n``b) ∙ ka = 126,5 ∙ 1 = 126,5 м/c
.
Ускорение точек S 2 и С находятся с помощью теоремы подобия.
Составляется пропорция, связывающая чертёжные размеры звена 2 (АВ , АС2 ) с отрезками плана ускорений:
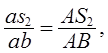
откуда определяется длинна неизвестного отрезка.
Этот отрезок откладывается на отрезке ab плана ускорений. Соединением полюса π с точкой s 2 получается отрезок π s 2 = 147,5 мм (определено замером).
Модуль ускорения точки s 2
aS 2 = (πs2 ) ∙ ka = 147,5 ∙ 1 = 147,5 мм/c.
Ускорение точки С определяются аналогично по принадлежности звену 3.
Определяются величины угловых ускорений звеньев 2 и 3 :
.
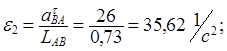
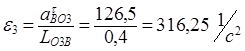Для определения направления ε2 отрезок n ` b плана ускорений устанавливается в точку В , а точка А закрепляется неподвижно; тогда становится очевидным, что ε2 направлена против часовой стрелки. Для определения направления ε3 отрезок n `` b плана ускорений устанавливается в точку В , а точка О3 закрепляется неподвижно; тогда становится очевидным, что ε3 направлена по часовой стрелке.
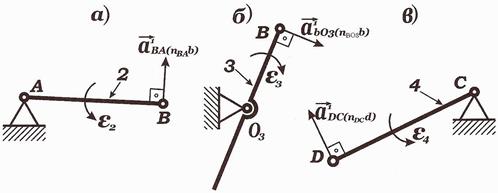
Рис. 5. Определение направлений угловых ускорений
Группа Ассура II 2 (4,5).
Внешними точками группы являются точки С и D 0 (точка D 0 принадлежит стойке), внутренней – точка D , принадлежащая звеньям 4 и 5 (в дальнейшем обозначается без индексов).
По принадлежности точки D звену 5 вектор её ускорения известен по направлению: 
D // x - x . Поэтому для построения плана ускорений для данной группы Ассура достаточно одного векторного уравнения:
.
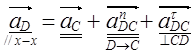В этом уравнении модуль нормального ускорения
На плане ускорений вектор 
изображается отрезком
