Курсовая работа: Синтез химико-технологической схемы

Лежащий в основе промышленного производства химико-технологический процесс представляет собой совокупность операций, позволяющих получить целевой продукт из исходного сырья. Любое химическое производство может быть представлено в виде трех блоков: подготовки и очистки сырья, химического превращения, выделения и очистки целевых продуктов. Эти блоки связаны между собой потоками вещества и энергии. Современная химическая технология разрабатывает и изучает совокупность физических и химических процессов и оптимальные пути их осуществления и управления ими в промышленном производстве различных веществ и материалов.

Количественное описание процессов химической технологии основано на законах химической термодинамики, переноса количества движения, теплоты и массы и химической кинетики. Анализ кинетических закономерностей единичных процессов, их взаимного влияния позволяет разработать технологический режим, т.е. оптимальную совокупность параметров (температура, давление, состав исходной реакционной смеси, природа катализатора), определяющих такие условия работы аппарата или системы аппаратов, которые позволяют получить наибольший выход продукта или обеспечить наименьшую его себестоимость. Математическое моделирование, широко используемое при расчетах химических процессов и оборудования, включает формализацию процесса в виде математической записи, задание различных значений режимных параметров системы для отыскания с помощью ЭВМ значения выходных параметров и экспериментальное установление адекватности модели изучаемому объекту. Оптимизация работы агрегатов осуществляется по экономическим и энерготехнологическим показателям. Если прежде при этом стремились достичь максимального результата по одному параметру, например, получить максимальный выход продукта, то теперь требуется оптимизация, включающая учет таких параметров, как энергетические и материальные ресурсы, защита окружающей среды, обеспечение заданного качества продуктов, безопасность процессов, продуктов и отходов производства.

Современное химическое предприятие – это сложная химико-технологическая система, состоящая из большого числа аппаратов и связей (потоков) между ними. Признание факта взаимного влияния агрегатов, составляющих ХТС, привело к необходимости рассматривать технологический процесс при его проектировании на основе системного подхода, когда химическое предприятие может быть представлено в виде многоуровневой иерархической структуры.

Основные этапы создания ХТС таковы. Первый уровень заканчивается составлением математических моделей элементов подсистем ХТС. Далее переходят к решению задач анализа, синтеза и оптимизации ХТС. Анализ состоит в изучении свойств и эффективности функционирования ХТС на основе ее математической модели. Свойства системы зависят как от параметров и характеристик состояния элементов (подсистем), так и от структуры технологических связей между элементами. Естественно, что полная модель может быть рассчитана лишь после того, как синтезирована ХТС, то есть анализ не может производиться в отрыве от синтеза. Задача синтеза заключается в создании ХТС, работающей с высокой эффективностью. Для этого необходимо, прежде всего, выбрать оптимальную технологическую топологию системы, которая определяет характер и порядок соединения отдельных аппаратов в технологической схеме. Очевидно, что с синтезом ХТС тесно связана задача оптимизации, которая сводится к нахождению экстремального значения выбранного критерия эффективности (как правило, экономического) функционирования системы. Из определения задач анализа, синтеза и оптимизации ХТС видно, что все эти этапы органически связаны друг с другом.

В данной работе производился синтез ХТС, состоящей из 5 реакторов, описываемых моделями идеального вытеснения, 2 абсорберов и системы теплообмена. Для получения статистической модели абсорберов по экспериментальным данным использовался метод Брандона. Для построения оптимальной системы теплообмена использовался эвристический метод оптимизации. Для получения адекватной модели реакторов по приведенным в задании данным таблицы 1 при нахождении значений k0 и E в уравнении Аррениуса использован метод наименьших квадратов. К работе прилагается условная схема ХТС, полученная на основе приведенных ниже расчетов. В конце даются выводы о возможных путях оптимизации ХТС, полученной на основе приведенного выше задания.

1. Практическая часть

1.1 Обработка экспериментальных данных

1.1.1 Нахождение параметров уравнения Аррениуса методом МНК

Зависимость константы скорости реакции k от температуры согласно закону Аррениуса выражается формулой:

, (1)

где k0 – предэкспоненциальный множитель; e = 2,718 – основание натуральных логарифмов; Ea– энергия активации, Дж/моль; R=8,315 – универсальная газовая постоянная, Дж/(моль*К); Т – абсолютная температура,К.

Значения k0 и Ea находят, измеряя значения константы скорости k при различных температурах Т. При этом получают набор из n пар значений kiэксп и Тi. Наиболее вероятными значениями k0 и E будут такие, которые при подстановке их величин в формулу (1) дадут значения kiрасч , наиболее близкие к kiэксп .

В общем виде эта задача может быть сформулирована так: имеются две переменные x и y, связанные некоторой зависимостью f, вид которой нам известен. В эту зависимость входят некоторые постоянные a и b, значения которых нам неизвестны. При переходе к логарифмической форме уравнения (1) и заменяя y=ln(k),x=1/T,a=-E/R,b=ln(k0), имеем линейную зависимость:

. (2)

Для того, чтобы найти наиболее вероятные значения a и b, мы провели серию измерений x и y, т.е. нашли n пар значений xiэксп и yiэксп. Требуется найти такие значения a и b, которые при подстановке в зависимость (2) совместно с xiэксп дали бы значения yiрасч, наиболее близкие к yiэксп. За меру близости берут величину:

. (3)

Требуется найти минимум функции s. Это достигается решением системы уравнений

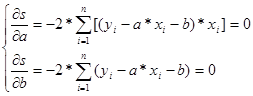(4)

Раскрывая знаки сумм и решая систему относительно неизвестных a и b, получаем формулы для нахождения наиболее вероятных значений a и b:

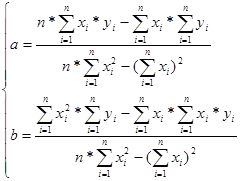(5)

Расчет значений a и b на основе данных таблицы 1 осуществлен с использованием электронных таблиц Excel(см. Приложение 1). Полученные значения: a=-7273,034, b=9,830637.

Применяя формулы k0=exp(b), E=-R*a, получаем экспериментальные значения параметров уравнения Аррениуса:

k0=18594,79, E=60468,01 Дж/(моль*К).

Практически всегда, кроме знания величин a и b, требуется определить и их погрешности Δa и Δb с некоторой степенью достоверности α. Поскольку измерения проводились с некоторой погрешностью, то yiрасч и yiэксп будут отличаться. Этот разброс характеризуется дисперсией s0, где

, (6)

где m=2 – количество определяемых констант.

Согласно Приложению 1 =0,001621.

Определение параметров a и b можно рассматривать как результат косвенных измерений. Для того, чтобы оценить точность определения параметра, можно воспользоваться законом накопления ошибок. Тогда дисперсии параметров a и b:

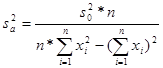, (7а)