Курсовая работа: Синтез химико-технологической схемы

=7991,043,=0,013721.

Погрешности определения параметров a и b:

, (8а)

, (8б)

где t – значение критерия Стьюдента для степени достоверности α (α=0,95) и степени свободы f=n-1.

Δa=199,3,Δb=0,26.

Погрешности определяемых k0 и E: Δk0=k0*Δb=4857,21; ΔE=R*Δa=1657,36.

1.1.2 Получение статистической модели абсорбера с помощью

метода Брандона

Сложный технологический процесс можно рассматривать как многомерный объект, на который действуют вектор входных параметров X и вектор управления Z. Выходные параметры составляют вектор выходных параметров Y. Общий вид статистической модели такого объекта в векторной форме

Y=f(X,Z). (9)

Для построения статистической модели абсорберов по данным таблицы 2 использовался метод Брандона (см. Приложение 2).

Сущность метода заключается в следующем. Предполагается, что функция F(x1,x2,…,xm) в формуле (9) является произведением функций от входных параметров, т.е.

, (10)

где yрi – расчетное значение i –го выходного параметра;

- средняя величина экспериментальных значений i – го выход-ного параметра;

n – количество опытов в исходной выборке.

При использовании метода Брандона важен порядок следования функций в уравнении (10). Чем больше влияние оказывает фактор на выходной параметр, тем меньшим должен быть его порядковый номер в указанном уравнении. Поэтому задача построения модели по методу Брандона разбивается на два этапа:

1. ранжирование влияющих факторов.

2. выбор вида зависимости и построение статистической модели.

Оценить степень влияния k-го фактора на выходной параметр можно по величине частного коэффициента множественной корреляции:

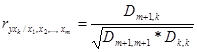, (11)

где - величина частного коэффициента корреляции, учитывающая влияние k-го фактора на выходной параметр y при условии, что влияние всех прочих факторов исключено; D- определитель матрицы, построенной из парных коэффициентов корреляции. Матрица имеет вид

Dm+1,k – определитель матрицы с вычеркнутыми m+1 строкой и k-м столбцом;

Dk,k , Dm+1,m+1 – определители матриц с вычеркнутыми k-м и (m+1)-м столбцом и строкой соответственно.

Порядок расположения влияющих факторов в уравнении (10) определяют в соответствии с убыванием величины частных коэффициентов корреляции.

В уравнении (10) каждая из функций f1(x1),f2(x2),…fm(xm) принимается либо линейной, либо нелинейной (степенной, показательной, экспоненциальной и т.д.)