Курсовая работа: Система лінійних однорідних алгебраїчних рівнянь Фундаментальна сукупність розвязків
0
1
0
0
0
1
0
1
0
1
0
0
0
1
Другий рядок таблиці (х3 +x5 , х4 +х5 , x3 , х4 , х5 ) є загальним розв'язком розглядуваної системи, якщо х3 , x4 та х5 є будь-які числа; третій — α1 = (1, 0, 1, 0, 0), четвертий — α2 = (0, 1, 0, 1, 0) та п'ятий — α3 = (1, 1, 0, 0, 1) є частинними розв'язками розглядуваної системи.
Останні рядки, тобто вектори α1 , α2 та α3 є лінійно незалежними, бо і лінійно незалежними є їх частини, відповідно, 
1 , 2 та 3 . Вектори α1 , α2 та α3 утворюють фундаментальну систему розв'язків розглядуваної нами в цьому завданні системи. Зауважимо, що ми здійснили такий вибір значень вільних невідомих, при якому одержано нормальну фундаментальну систему α1 , α2 та α3 розв'язків заданої системи рівнянь.
Завдання 2. Знайти фундаментальну систему розв'язків.
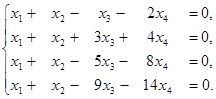
Розв'язання. Кожна система лінійних однорідних рівнянь є сумісною. Знаходимо ранг матриці А цієї системи.
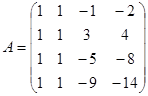
Матриця А — ненульова, отже, 
Обчислюємо мінори третього порядку матриці А, одержані обведенням відмінного від нуля мінора 
другого порядку. Бачимо, що перший і другий рядки однакові, тому нам досить обчислити два мінори третього порядку утворені обведенням першого стовпця і третього рядка, першого стовпця і четвертого рядка.
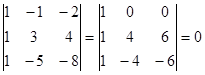, тому що другий і третій рядки пропорційні.
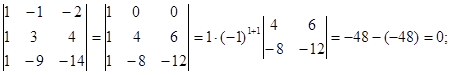
Таким чином, ранг матриці А дорівнює 2. Зважаючи на те, що її базовий мінор розташовано в правому верхньому куті матриці А, залишаємо в системі тільки перші два рівняння, а в їх лівих частинах — тільки ті невідомі, коефіцієнти при яких ввійшли до базового мінору. Інші дві невідомі переносимо в праві частини, тобто вільними невідомими є х3 та х4 . Маємо:
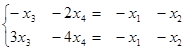
Додамо до другого рівняння перше помножене на 3
