Курсовая работа: Системи модульно-розвивального навчання

Ключова задача 2 . «Середини сторін чотирикутника».

Середини сторін опуклого чотирикутника є вершинами паралелограма, площа якого дорівнює половині площі даного чотирикутника.

Розв‘язання:

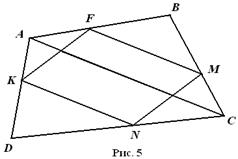
Відрізки FM і KN (рис.5) є середніми лініями трикутників ABC і ADC відповідно. Тоді FM׀׀AC, і KN׀׀AC, .Звідси FM=KN, FM׀׀KN , і отже, чотирикутник FMNK – паралелограм. Нехай площа чотирикутника ABCD дорівнює S. і .Звідси .

Аналогічно . Одержуємо

.

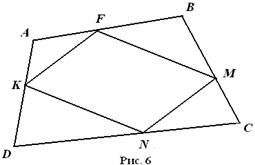
Приклади:Задача 4. Довести, що в опуклому чотирикутнику сума квадратів діагоналей вдвічі більша за суму квадратів відрізків, що сполучають середини протилежних сторін.

Розв’язання:

Скориставшись теоремою про сторони і діагоналі паралелограма, маємо: (рис. 6). Враховуючи, що ,

одержуємо

.

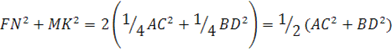Задача 5. Діагоналі трапеції взаємно перпендикулярні, довжина однієї з них дорівнює 6 см. Довжина відрізка, що з’єднує середини основ, дорівнює 4,5 см. Знайти площу трапеції.

Розв’язання: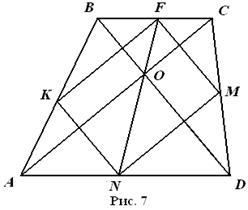

Нехай K і N (рис. 7) –середини бічних сторін трапеції ABCD. FN=4,5 см, AC=6 см і BOA=90⁰ . Оскільки KF׀׀AC і KN׀׀BD, то кут NKF прямий і KFMN – прямокутник. Тоді з прямокутного трикутника FKN одержуємо: . , а оскільки , то .

Застосовуючи метод ключової задачі, можна значно активізувати самостійно-навчальну діяльність учнів в процесі розв’язування планіметричних задач, а також ліквідувати перевантаження старшокласників, адже вони розв’язують меншу кількість задач як в класі, так і вдома.

Однак знання тільки алгоритму розв’язування ключових задач не може задовольнити тих учнів, які проявляють інтерес до математики. У роботі з ними важливо вчасно перейти до розбору задач нестандартних.

Слід відмінити важливість консультацій. Їх мета навчити учнів задумуватись над проблемою, усвідомити для себе, які виникли труднощі при знайомстві з темою, а для розв’язання цих труднощів – сформулювати питання, в яких він би хотів одержати відповідь.

На контрольно-смисловому модулі вчитель використовує понятійні і математичні диктанти , кросворди, тестові завдання, застосовує таку форму навчання, як співбесіда.

Співбесіда дозволяє через доцільно – складену систему запитань з теми з’ясувати рівень засвоєння вивченого матеріалу кожним учнем.Якщо виявляється недостатня підготовка учнів, то здійснюється індивідуальна робота, призначаються консультації на допомогу цим учням. Проводити заняття вчителю допомагає група асистентів (перевіряють самостійні роботи, виставляють оцінки в контрольний аркуш).

Оскільки мета адаптивно-перетворюючого етапу – формування умінь, навичок і норм діяльності, застосування знань у нестандартних ситуаціях, то на цьому етапі педагог практикує такі форми навчання, я