Курсовая работа: Средние величины и показатели вариации

В данном случае следует воспользоваться формулой средней арифметической взвешенной, поскольку данные вторичные. Интервальные значения признака встречаются не один раз (т.е. повторяются) и эти числа повторений (частоты) не одинаковы.

Конкретными значениями признака, которые должны непосредственно участвовать в расчетах служат середины (центры) интервалов, весами – частоты.

Данный результат отличается от результата, полученного на основе средней арифметической простой. Это объясняется тем, что на основе ряда распределения мы уже не располагаем исходными индивидуальными данными, а вынуждены ограничиться лишь сведениями о величине середины (центра) интервала.

Пример 4.6. Просроченная задолженность по кредитам предприятиями фирмы за отчетный год характеризуется следующими данными:

№ предприятия фирмы	Задолженность по кредитам, тыс. руб.	Удельный вес просроченной задолженности, %
1 2 3	3500 4000 2000	15 30 20	52500 120000 40000
Итого	9500	212500

Определить средний процент просроченной задолженности фирмы.

Решение: Основой расчета является экономическое содержание показателя.

Удельный вес Объем просроченной задолженности

просроченной = -------------------------------------------------------- ∙ 100

задолженности, , % Объем общей задолженности

Для расчета среднего процента просроченной задолженности фирмы в этом случае воспользуемся формулой средней арифметической взвешенной:

%.

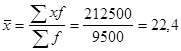3. Средняя гармоническая и условия ее применения

Среднюю гармоническую взвешенную следует использовать в тех случаях, когда, кроме вариант осредняемого признака , известны показатели, представляющие собой произведения вариант на их частоты . Величиной может быть, например, товарооборот по видам товаров при расчете средней их цены, фонды заработной платы у отдельных категорий работников при расчете средней заработной платы; стоимостные объемы сделок при покупке валют, ценных бумаг, биржевых продаж и т.д. Как видим, ситуаций, когда нам известны не частоты, а произведения частот на соответствующие им варианты при расчете средней величины, более чем достаточно.

Формула средней гармонической взвешенной имеет вид:

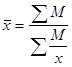(6)

где - значения произведений варианты на соответствующую ей частоту;

- значения вариант.