Курсовая работа: Статистическое изучение основных фондов

2. Постройте графики полученного ряда распределения. Графически определите значения моды и медианы. По данным таблицы 1 строим гистограмму распределения предприятий по эффективности использования основных производственных фондов (рис.1).

Рис. 1. Гистограмма распределения предприятий по эффективности использования основных производственных фондов.

Далее, соединяя середины верхних оснований столбцов, получаем полигон распределения.

Теперь графически необходимо определить значения моды и медианы. Мода – это наиболее часто встречающаяся варианта совокупности. На графике она будет выглядеть так (рис.2.):

Рис. 2. Мода

Медиана – это варианта, делящая ряд пополам. Для её графического изображения построим кумуляту и рассчитаем кумулятивно – накопленные частоты в таблице. (таблица 2)

Таблица 2. Кумулятивно - накопленные частоты использования основных производственных фондов.

Группы предприятий по эффективности использования основных производственных фондов, млн. руб.	Число предприятий в группе	Кумулятивно – накопленные частоты
0.9 – 0.98	3	3
0.98 – 1.06	7	10
1.06 – 1.14	11	21
1.14 – 1.22	5	26
1.22 – и более	4	30

Рис.3. Кумулятор распределения предприятий по эффективности использования основных производственных фондов

Модальным будет являться третий интервал, так как его кумулятивная частота равна 21 (3+7+11), что превышает половину суммы всех частот (30/2=15). (Рис. 3.)

Вывод: медиана = 1.07 млн. руб. показывает, что половина предприятий имеет эффективность использования основных производственных фондов < 1.07 млн. руб., а вторая >1.07 млн. руб. Мода показывает, что наибольшее часто встречаются в совокупности предприятия с эффективностью использования основных производственных фондов 1.09-1.14 млн. руб.

3. Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.

По данным интервального ряда составим расчетную таблицу 3.

Таблица 3. Расчётная таблица

Группы предприятий по эффективности использования основных производственных фондов, млн. руб.	Число предприятий в группе	Середина интервала Xi
0.9 – 0.98	3	0.94	0.0256	0.0768
0.98 – 1.06	7	1.02	0.0064	0.0448
1.06 – 1.14	11	1.1	0	0
1.14 – 1.22	5	1.18	0.0256	0.032
1.22 – и более	4	1.26	0.0064	0.1024

3. 1. Находим середины интервалов Xi:

1) (0.9+0.98)/2=0.94; 2) (1.06+1.14)/2=1.1; 4) (1.14+1.22)/2=1.18; 5)

(1.22+1.3)/2=1.26

3. 2. Так как у нас имеются сгруппированные данные, представленные в виде интервального ряда распределения, то для нахождения средней арифметической и среднего квадратического отклонения будем использовать формулы для взвешенной средней:

где ∑f_i – это общая численность единиц совокупности; ∑X_i * f_i – это сумма произведений величины признаков на их частоты.

Следовательно,

X_{ар. взв.} =(0.94*3+1.02*7+1.1*11+1.18*5+1.26*4)/30=1.1млн. руб.

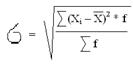
Для вычисления среднего квадратического отклонения необходимо вычислить некоторые составляющие формулы: (X_i – X)² и (X_i – X)² * f. (таблица 3).

1) (0.94-1.1)² = 0.0256; 2) (1.02-1.1)² = 0.0064; 3) (1.1-1.1)² = 0; 4) (1.18-1.1)² = 0.0064; 5) (1.16-1.1)² = 0.0256.

1) 0.0256*3 = 0.0768; 2) 0.0064*7 = 0.0448; 3) 0*11 = 0;4) 0.0064*5 = 0.032; 5) 0.0256*4 = 0.1024.

Подставляем найденные значения в исходную формулу среднего квадратического отклонения, получаем:

млн. руб.