Курсовая работа: Структурная схема и управление электроприводом
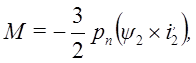(10)
Учитывая выражения (8), можно записать (9) и (10) в виде
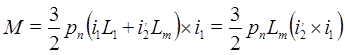; (11)
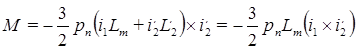. (12)
Вторые равенства в уравнениях (11), (12) справедливы потому, что векторное произведение двух одинаково направленных векторов равно нулю.
Для полного описания переходных процессов в асинхронном электродвигателе к уравнениям напряжений и моментов следуй добавить уравнение
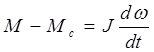, (13)
записанное для скалярных значений моментов М и Мс .
Полученная система уравнений электродвигателя является нелинейной, и решение ее для различных динамических режимов работы электродвигателя может быть выполнено с использованием вычислительных машин. При синтезе систем управления асинхронным электродвигателем целесообразно располагать простыми и наглядными динамическими моделями электродвигателя в виде передаточных функций или структурных схем. Такая возможность появляется, если рассматривать переходные процессы в отклонениях относительно начальных координат электродвигателя.
Сравнительно простая структурная схема может быть получена, если пренебречь активным сопротивлением статорной цепи, т. е. положить R1 =0. Безусловно, что такое пренебрежение накладывает определенные ограничения на использование получаемых моделей. Они вполне применимы для систем с небольшим диапазоном регулирования скорости относительно синхронной скорости, для электродвигателей средней и большой мощности. При широком регулировании скорости, а также для электродвигателей малой мощности необходимы уточнения структурных схем.
Для дальнейших исследований динамических свойств асинхронных ^ электродвигателей целесообразно результирующие векторы представить в виде проекций на комплексной плоскости и записать их через вещественные и мнимые части в следующем виде:
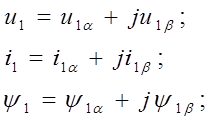
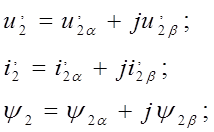(14)
Совместив вектор напряжения статора с действительной осью координатной системы, т. е. положив u1 β =0, на основании (7) получим
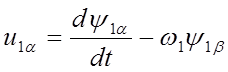; (15)
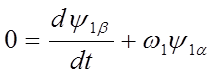; (16)
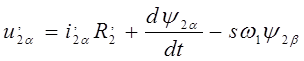; (17)
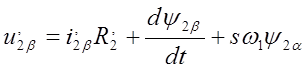. (18)
Выразив также электромагнитный момент по уравнению (9) через составляющие векторов тока и потокосцепления
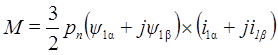
и применив правило векторного произведения векторов, получим абсолютное значение момента:
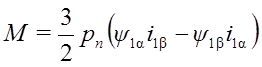, (19a)
где 
;
Воспользовавшись выражением (10), можно аналогично получить
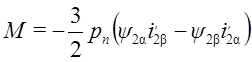(19б)
где 
;
Составляющие тока ротора могут быть выражены через составляющие потокосцепления в следующем виде:
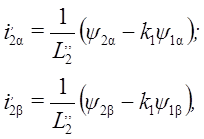(20)