Курсовая работа: Сущность и методика деления постоянных и переменных затрат

Основными статистическими методами дифференциации общей суммы затрат на постоянные и переменные расходы являются:

- метод минимальной и максимальной точки (метод мини-макси);

- графический (статистический) метод;

- метод наименьших квадратов.

При методе мини-макси из всей совокупности данных выбирают два периода с наименьшим и наибольшим объемом производства. Затем определяется ставка переменных затрат, или средние переменные издержки, в себестоимости единицы продукции. Общая сумма постоянных расходов исчисляется как разность между общей суммой затрат отчетного периода и произведением их переменной части на соответствующий объем производства.

Пример 2.

За семь месяцев предприятие имело следующие объемы производства и затраты на электроэнергию (табл.2).

Таблица 2.

Динамика объемов производства и затрат на электроэнергию

Месяц	Объем производства, Х, ед.	Расходы на электроэнергию, Rвал, руб.
I	18	7400
II	16	7100
III	22	8000
IV	24	9000
V	25	10000
VI	20	7500
VII	15	7000
Итого	140	56000
В среднем в месяц	20	8000

Требуется определить переменные расходы на единицу объема, величину постоянных затрат и составить уравнение валовых издержек.

Графический (статистический) метод основан на том, что общую сумму затрат можно представить уравнением первой степени: ,которому соответствует график (рис. 2.1.).

На графике наносятся данные об общих затратах при разных объемах производства. Затем «на глазок» проводится длина. Точка ее пересечения с осью У показывает уровень постоянных расходов. Переменные расходы определяют как разность между Rвал и Rfix, деленную на средний объем производства. Ставка переменных затрат: (8000 – 2600) : 20 = 5400 : 20 = 270 (руб.). Следовательно, Rвал = 2600 + 270Х.

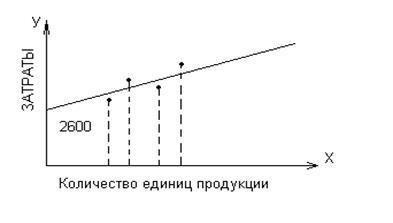
Рис. 2.1. График статистической зависимости общей суммы затрат от объема производства

Дифференциация затрат методом наименьших квадратов дает наиболее точные результаты.

Пример 3.

Рассмотрим применение метода наименьших квадратов для данных примера 2 (табл. 3).

Таблица 3.

Динамика валовых расходов и объемов производства (продаж)

Месяц	Х	Rвал	Х2	Х · Rвал
I	18	7400	324	133200
II	16	7100	256	113600
III	22	8000	484	176000
IV	24	9000	576	216000
V	25	10000	625	250000
VI	20	7500	400	150000
VII	15	7000	225	105000
Итого	140	56000	2890	1143800

Величина переменных затрат на единицу продукции rv определяется исходя из соотношений:

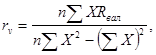(3)

где n – количество периодов, на основе которых исчисляется величина постоянных и переменных издержек.

Общую сумму постоянных расходов рассчитываем по формуле

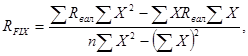(4)

Подставляя соответствующие значения в формулы (3) и (4), получим:

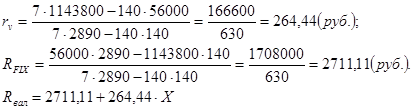
Выводы и предложения