Курсовая работа: Сущность метода Монте-Карло и моделирование случайных величин
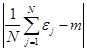 .
.
Для получения случайных чисел используют обычно три способа: таблицы случайных величин, генераторы случайных чисел и метод псевдослучайных чисел.
Таблицы случайных чисел используют предпочтительно при расчётах вручную. Определяющую роль в этом играют два факта: 1) при использовании ЭВМ легче и удобней воспользоваться генератором случайных чисел, получаемых тут же, чем загружать из памяти значения таблицы, которая к тому же, будет занимать там место. 2) При подсчёте вручную нет необходимости использовать ЭВМ, так как часто необходимо выяснить лишь порядок искомой величины.
Генераторы случайных чисел анализируют какой-либо процесс, доступный для них (шумы в электронных лампах, скачки напряжения) и составляют последовательность из 0 и 1, из которых составляются числа с определёнными разрядами, однако такой метод получения случайных величин имеет свои недостатки. Во-первых, трудно проверить вырабатываемые числа. Проверки приходится делать периодически, так как из-за каких-либо неисправностей может возникнуть так называемый дрейф распределения (нули и единицы в каком-либо из разрядов станут появляться не одинаково часто). Во-вторых, обычно все расчёты на ЭВМ проводятся несколько раз, чтобы исключить возможность сбоя. Но воспроизвести те же самые случайные числа невозможно, если их только не запоминать по ходу счёта. А если запоминать, то снова появляется случай таблиц.
Таким образом, самым эффективным способом получения случайных чисел – это использование псевдослучайных чисел.
Числа, получаемые по какой-либо формуле и имитирующие значения случайной величины ![]() , называются псевдослучайными числами.
, называются псевдослучайными числами.
Первый алгоритм для получения псевдослучайных чисел был предложен Дж. Нейманом. Он называется методом середины квадратов.
Пусть задано 4-значное число ![]() . Возведём его квадрат. Получим 8-значное число
. Возведём его квадрат. Получим 8-значное число ![]() . Выберем 4 средние цифры этого числа и положим
. Выберем 4 средние цифры этого числа и положим ![]() .Далее
.Далее ![]() и т.д.
и т.д.
Но этот алгоритм не оправдал себя, так как получается слишком много малых значений. Поэтому были разработаны другие алгоритмы. Наибольшее распространение получил алгоритм, называемый методом сравнений (Д. Лемер): определяется последовательность целых чисел ![]() , в которой начальное число
, в которой начальное число ![]() задано, а все последующие числа
задано, а все последующие числа ![]() вычисляются по одной и той же формуле
вычисляются по одной и той же формуле
![]() при
при ![]() (1.8)
(1.8)
По числам ![]() вычисляются псевдослучайные числа
вычисляются псевдослучайные числа
![]() (1.9)
(1.9)
Формула (1.8) означает, что число ![]() равно остатку, полученному при делении
равно остатку, полученному при делении ![]() на
на ![]() , такой остаток называют наименьшим положительным вычетом по модулю
, такой остаток называют наименьшим положительным вычетом по модулю ![]() Формулы (1.8), (1.9) легко реализовать на ЭВМ.
Формулы (1.8), (1.9) легко реализовать на ЭВМ.
Достоинства метода псевдослучайных чисел довольно очевидны. Во-первых, на получение каждого числа затрачивается всего несколько простых операций, так что скорость генерирования случайных чисел имеет тот же порядок, что и скорость работы ЭВМ. Во-вторых, программа занимает не так много места в памяти. В-третьих, любое из чисел ![]() может быть легко воспроизведено. В-четвёртых, необходимо лишь один раз проверить «качество» такой последовательности, затем её можно много раз безбоязненно использовать при расчёте однотипных задач.
может быть легко воспроизведено. В-четвёртых, необходимо лишь один раз проверить «качество» такой последовательности, затем её можно много раз безбоязненно использовать при расчёте однотипных задач.
Единственный недостаток метода – ограниченность количества псевдослучайных чисел, так как если последовательность чисел ![]() вычисляется на ЭВМ по формуле вида
вычисляется на ЭВМ по формуле вида
![]()
то эта последовательность обязательно периодическая. Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел.
Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет случайная величина ![]() , равномерно распределённая в
, равномерно распределённая в ![]() . Процесс нахождения значения какой-либо случайной величины
. Процесс нахождения значения какой-либо случайной величины ![]() путём преобразования одного или нескольких значений
путём преобразования одного или нескольких значений ![]() называется разыгрыванием случайной величины
называется разыгрыванием случайной величины ![]() .
.
Допустим, что необходимо получать значения случайной величины ![]() , распределённой в интервале
, распределённой в интервале ![]() , с плотностью
, с плотностью ![]() . Докажем, что значения
. Докажем, что значения ![]() можно находить из уравнения
можно находить из уравнения
![]() (1.10)
(1.10)
т.е. выбрав очередное значение ![]() , надо решить уравнение (1.10) и найти очередное значение
, надо решить уравнение (1.10) и найти очередное значение ![]() .
.
Для доказательства рассмотрим функцию
![]() .
.
Из общих свойств плотности (1.2), (1.3) следует, что
![]()
Значит, функция ![]() монотонно возрастает от 0 до 1, и любая прямая
монотонно возрастает от 0 до 1, и любая прямая ![]() , где
, где ![]() , пересекает график
, пересекает график ![]() в одной единственной точке, абсциссу которой мы и принимаем за
в одной единственной точке, абсциссу которой мы и принимаем за ![]() . Таким образом, уравнение (1.10) всегда имеет одно и только одно решение.
. Таким образом, уравнение (1.10) всегда имеет одно и только одно решение.
Выберем теперь произвольный интервал ![]() , содержащийся внутри
, содержащийся внутри ![]() . Точкам этого интервала
. Точкам этого интервала ![]() отвечают ординаты кривой
отвечают ординаты кривой ![]() , удовлетворяющие неравенству
, удовлетворяющие неравенству ![]() .
.
Поэтому, если ![]() принадлежит интервалу
принадлежит интервалу ![]() , то
, то ![]() принадлежит интервалу
принадлежит интервалу ![]() , и наоборот. Значит
, и наоборот. Значит ![]()
Так как ![]() равномерно распределена в
равномерно распределена в ![]() , то
, то