Курсовая работа: Сущность метода Монте-Карло и моделирование случайных величин

Выберем равномерно распределённых на отрезке последовательностей случайных чисел

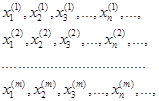
Тогда точки можно рассматривать как случайные, равномерно распределённые в мерном единичном кубе.

Пусть из общего числа случайных точек точек попали в область G, остальные оказались вне G. Тогда при достаточно большом имеет место приближенная формула:

(3.2)

где под понимается мерный объём области интегрирования. Если вычисление объёма затруднительно, то можно принять , и для приближенного вычисления интеграла получим:

(3.3)

Указанный способ можно применить к вычислению кратных интегралов и для произвольной области , если существует такая замена переменных, при которой новая область интегрирования будет заключена в мерном единичном кубе.

Второй способ.

Если функция , то интеграл (3.1) можно рассматривать как объём тела в мерном пространстве, т.е.

(3.5)

где область интегрирования определяется условиями

Если в области , то введя новую переменную , получим

где область лежит в единичном мерном кубе

Возьмём равномерно распределенных на отрезке случайных последовательностей

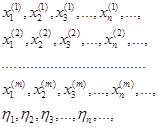
Составим соответствующую последовательность случайных точек

Пусть из общего числа случайных точек точек принадлежат объёму , тогда имеет место приближенная формула

(3.6)

2. Практическая часть

2.1 Пример 1

Вычислим приближенно интеграл

Точное значение его известно:

Используем для вычисления две различные случайные величины , с постоянной плотностью (т.е. равномерна распределена в интервале ) и с линейной плотностью .Линейная плотность более соответствует рекомендации о пропорциональности и . Поэтому следует ожидать, что второй способ вычисления даст лучший результат.

1) Пусть , формула для разыгрывания имеет вид . А формула (2.2) примет вид .

Пусть . В качестве значений используем тройки чисел из табл. 1 (см. приложение), умноженные на 0.001. Промежуточные результаты сведены в табл. 2.1. Результат расчёта

Таблица 2.1

	1	2	3	4	5	6	7	8	9	10
	0.865	0.159	0.079	0.566	0.155	0.664	0.345	0.655	0.812	0.332
	1.359	0.250	0.124	0.889	0.243	1.043	0.542	1.029	1.275	0.521
	0.978	0.247	0.124	0.776	0.241	0.864	0.516	0.857	0.957	0.498