Курсовая работа: Теорема Дезарга и её применение к решению задач из курса школьной геометрии
![]() - линейно зависимы Þ точки А', С', Q ' Î одной прямой.
- линейно зависимы Þ точки А', С', Q ' Î одной прямой.
Следовательно, Q =АС Ç А'С'
![]() –
– ![]() =
=![]()
![]() –
– ![]() =
= ![]() (3)
(3)
![]() ,
,![]() ,
,![]() – линейно зависимы Þ точки В, С, R Î одной прямой.
– линейно зависимы Þ точки В, С, R Î одной прямой.
![]() ,
,![]() ',
', ![]() ' – линейно зависимы Þ точки В', С', R ' Î одной прямой
' – линейно зависимы Þ точки В', С', R ' Î одной прямой
Следовательно, R =ВС Ç В'С'.
Составим выражение: ![]()
![]() =
=![]() -
- ![]() -
-![]() +
+ ![]() +
+ ![]() -
- ![]() =
=![]()
![]() - векторы
- векторы ![]() ,
, ![]() ,
, ![]() линейно зависимы Þ точки P , Q , R лежат на одной прямой.
линейно зависимы Þ точки P , Q , R лежат на одной прямой.
Теорема доказана.
Если точки пересечения соответственных сторон двух трехвершинников лежат на одной прямой, то прямые, проходящие через соответственные вершины этих трехвершинников, проходят через одну точку.
Доказательство при помощи теоремы Менелая
Теорема Менелая гласит:
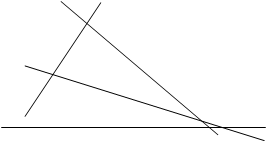
Если точки X, Y, Z лежащие на сторонах ВС, СА, АВ (соответственно продолженных) треугольника АВС коллинеарны, то
![]() .
.
Обратно, если это уравнение выполняется для точек X, Y, Z, лежащих на трех сторонах треугольника, то эти три точки коллинеарны.
 |
 |
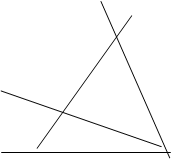
Теорема Дезарга: Если два треугольника перспективны относительно точки и если их пары соответствующих сторон пересекаются, то эти три точки пересечения коллинеарны.
Доказать: P, Q, Rколлинеарны
Доказательство: Мы имеем теорему лишь о принадлежности точек прямым и пересечении прямых. Треугольники АВС и A’B’C’ перспективны относительно точки О, а пары их соответствующих сторон пересекаются в точках R, Q, P. Для доказательства применим теорему Менелая к тройкам точек. {Q, C’, A’}, {R, B’, C’}, {P, A’, B’}
Лежащих на сторонах трех треугольников ![]() ОАС,
ОАС, ![]() ОСВ,
ОСВ, ![]() ОВА , получим при этом
ОВА , получим при этом
![]() ,
,
![]() ,
,
![]()
Перемножим эти три выражения и, проделав умеренное число сокращений, получим
![]() ,
,
Þ Точки Q , R , P коллинеарны.
Теорема доказана.
Доказательство в проективной системе координат
На проективной действительной плоскости имеет место Теорема Дезарга.
Теорема Дезарга: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой. P = AB Ç A ' B ', Q = AC Ç A ' C ', R = BC Ç B ' C ', AA ' Ç BB ' Ç CC '= Q