Курсовая работа: Теорема Дезарга и её применение к решению задач из курса школьной геометрии

Доказательство: Введем проективную систему координат, примем точки А, В, С, О за фундаментальные: А (1,0,0), В (0,1,0), С (0,0,1), О (1,1,1)

Координаты точки А' – есть линейная комбинация координат точки А и точки О , так как А ¹ А' , то А'= a А + d q

Можно положить d=1. Тогда получаем А'= a А + q . Тоже самое относится и к другим вершинам трехвершинника A ' B ' C ' . Поэтому А' ( a +1,1,1), В' (1, b +1,1), С' (1,1, g +1) уравнение прямой АВ :

АВ: х₃ =0

Уравнение А ¢ В ¢ :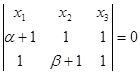

А ¢ В ¢ :

А ¢ В ¢ :

Так как АВ А ¢ В ¢ =Р ,

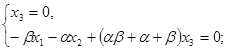
P :

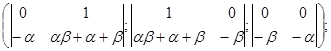P : P .

АС: 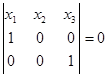, A ¢ C ¢ :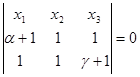

АС: х₂ =0

A ¢ C ¢ :

так как АС A ¢ C ¢ =Q

Q:,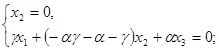

то Q

ВС: 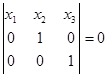, B ¢ C ¢ :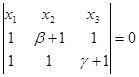

так как R=BC∩B¢C¢

R :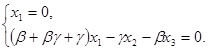, то R .

С помощью условия коллинеарности трех точек убедимся, что точки P, Q, R лежат на одной прямой.

Имеем

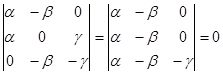
Условие коллинеарности выполнено, следовательно, P , Q , R Î одной прямой.

Теорема доказана.

2. Применение теоремы Дезарга к решению задач

2.1 Использование теоремы Дезарга на евклидовой плоскости

В аксиоматическом построении проективной плоскости мы рассматриваем теорему Дезарга, как аксиому. Покажем, что она справедлива на евклидовой плоскости. Если две одинаковые конфигурации, составленные из точек и прямых, могут быть приведены в соответствие так, что пары соответствующих точек соединяются прямыми, пересекающимися в одной точке, то мы говорим, что эти две конфигурации перспективны относительно этой точке. Если соответствие таково, что пара соответствующих прямых пересекаются в точках лежащих на одной прямой, то говорим, что эти две конфигурации перспективны относительно этой прямой.

Сформулируем теорему Дезарга, покажем использование на евклидовой плоскости. При доказательстве будем пользоваться теоремой Менелая.