Курсовая работа: Теорема Гурвица и ее приложение

;

, если ; , если .

Подпространство- такое подмножество пространства L, которое само является пространством.

Ортонормированный базис: Говорят, что элементов -мерного евклидова пространства образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если

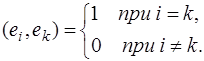
Билинейное отображение: Пусть L-линейное пространство над полем Р. Тогда отображение называется билинейным, если

,

Сюръективное отображение- отображение , которое каждому элементу из сопоставляет, по крайней мере, один прообраз, т.е. .

Ядро: Пусть - гомоморфизм кольца R в кольцо S. Множество , где 0’-нуль в S, -ядро.

Обратимая матрица- матрица, для которой существует обратная матрица.

Невырожденная матрица - квадратная матрица, определитель которой отличен от нуля.

Симметричная матрица - матрица является симметричной, если она совпадает со своей транспонированной матрицей (т.е. A = A'). Другими словами, нижний треугольник квадратной матрицы является "зеркальным отражением" верхнего треугольника.

Характеристика поля - пусть P-поле. Если существует такое целое положительное n, что для каждого выполняется равенство n·r=0, то наименьшее из таких чисел n называется характеристикой поля P. Обозначение - char P.

Кососимметричная матрица- квадратная матрица А над полем P характеристики такая, что, где — транспонированная матрица.

Линейная независимость системы векторов: Система векторов называется линейно независимой , если существует только тривиальная линейная комбинация данных векторов равная нулевому вектору.

3. Теорема Ферма

Какие целые числа можно представить в виде суммы квадратов двух целых чисел? Это один из самых старых вопросов теории чисел, восходящий, по крайней мере, к Диофанту. Полный ответ на данный вопрос дал Пьер де Ферма (французский математик, 17 августа 1601 — 12 января 1665). Напишем первые несколько целых чисел, представимых в виде суммы квадратов

0; 1; 2; 4; 5; 8; 9; 10; 13; 16; 17; 18; 20; 25; 26; 29; 32; 34; 36; 37; 40; 41; 45;

49; 50; 52; 53; 58; 61; 64; 65; 68; 72; 73; 74; 80; 81; 82; 85; 89; 90; 97; 98; 100

Можно сделать несколько экспериментальных выводов. Во-первых, не каждое число представимо в виде суммы двух квадратов. Например, 3, 6, 11, 12 не представляются в таком виде. Более того, можно заметить, что ни одно число вида 4к+3 не представляются в виде суммы двух квадратов (при целом к). Во-вторых, если каждое из двух чисел является суммой квадратов, то таково и их произведение. Можно сделать и другие заключения.

Остановимся более детально на втором заключении и попробуем обосновать его. Справедлива формула

(1)

Действительно,

и

Из этой формулы, в частности, вытекает, что если каждое из чисел a и b можно представить как сумму квадратов двух целых чисел, то их произведение тоже представимо в таком виде. Формула (1) является простым следствием коммутативного, ассоциативного и дистрибутивного законов.