Курсовая работа: Теория нелинейной теплопроводности

(4.5)

если предположить, что

т.е. (4.6)

Тогда

(4.7)

Так как условие (4.5) должно выполняться для любых r и t, то это возможно лишь при S(t) = 0. С учетом формулы (4.7) это условие приводит к дифференциальному уравнению для определения функции А(t):

(4.8)

Для обеспечения слабой сходимости решения в форме (4.3) при к дельтаобразному начальному распределению необходимо, чтобы , а при . Разделяя переменные в уравнении (4.8), интегрируя и полагая константу интегрирования равной нулю, находим решение.

(4.9)

неограниченно возрастающее при .

Теперь, используя соотношение (4.6), для функции l(t) приходим к следующему дифференциальному уравнению:

(4.10)

Общее решение этого неоднородного дифференциального уравнения первого порядка находим как сумму общего решения однородного уравнения и частного решения неоднородного уравнения. В результате получаем

(4.11)

Таким образом, с учетом уравнений (4.3), (4.9) и (4.11) решение исходной задачи (4.2) можно записать в форме фронтового решения

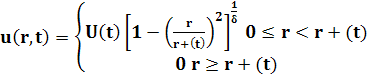(4.12)

где

(4.13)

(4.14)

Значение константы С в формуле (4.14) можно найти из соотношения

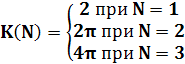(4.15)

являющегося следствием начального условия задачи Коши (4.2). С учетом выражений (4.12) - (4.14) соотношение (4.15) преобразуется к виду

(4.16)

Учитывая, что

а значение интеграла