Курсовая работа: Теория нелинейной теплопроводности

из выражения (4.16) находим значение константы

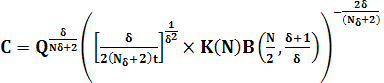(4.17)

Таким образом, точное решение задачи (4.2) имеет вид (4.12), где u(t) и r+(t) определены соотношениями (4.13) и (4.14) с константой С, которая находится по формуле (4.17). Найденное решение допускает предельный переход р 0. Полагая в уравнении (4.14) р = 0, получаем решение задачи о влиянии мгновенного сосредоточенного теплового источника в нелинейной среде без объемного поглощения. Для N = 1 это решение было построено нами ранее.

Дадим физическую интерпретацию решения (4.12). Оно описывает эволюцию тепловой структуры конечных пространственных размеров, которую мы будем называть тепловым импульсом. В любой момент времени t > 0 существует фронт теплового импульса r = r+(t), отделяющий область тепловых возмущений от невозмущенной области, куда тепловые возмущения еще не дошли и где u = 0.

Проанализируем характер движения фронта теплового импульса. Для этого запишем уравнение (4.14) в виде

(4.18)

Где

Качественный вид зависимости (4.18) представлен на рисунке.

Рисунок 3 описывает качественный вид зависимости движения фронта теплового импульса

На начальной стадии эволюции теплового импульса механизм тепловой диффузии является определяющим и пространственный размер теплового импульса увеличивается с течением времени. В среде распространяется волна разогрева. Затем скорость движения фронта теплового импульса уменьшается, и при t = t*, где

фронт останавливается, проникнув в нелинейную среду с объемным поглощением лишь на конечную глубину.

При t > t* объемное поглощение тепловой энергии становится доминирующим фактором в балансе энергии, и волна разогрева сменяется волной охлаждения, когда ширина теплового импульса уменьшается. Фронт теплового импульса изменяет направление движения, и в момент времени t = tm тепловой импульс стягивается в точку, прекращая свое существование. Тепловой импульс в среде с объемным поглощением тепловой энергии существует конечное время, т.е. для t > tm в любой точке пространства u = 0. Такую локализацию тепловых возмущений с конечным временем их существования в нелинейной среде с поглощением естественно назвать пространственно-временной локализацией.

При р = 0, т.е. в отсутствие объемного поглощения теплоты, из уравнения (4.14) следует монотонный степенной рост ширины теплового импульса (штриховая линия на рисунке 2). Тепловые возмущения в этом случае проникают в среду неограниченно далеко.

Полученные соотношения можно рассматривать и при р < 0, когда в объеме среды протекают экзотермические процессы, приводящие к выделению тепловой энергии. В такой нелинейной среде с объемными тепловыми источниками фронт теплового импульса распространяется с конечной скоростью, однако ширина теплового импульса в соответствии с соотношением (4.14) при р < 0 увеличивается.

5. Решения нелинейной задачи теплопроводности на полупрямой

Начнем с рассмотрения задачи

(5.1)

с начальным/граничным условием для уравнения на полупрямой характеризуемой начальным и граничными условиями

u(x,0)=u0(x) ∞˃x≥0 (5.2)

ux(∞,t)=0 (5.3)

(5.4)

где – положительная константа, а – интегрируемая функция. Граничное условие (5.4) представляет заданную теплопроводность в начале координат

Введем преобразование годографа

(5.5)

(5.6)