Курсовая работа: Теория нелинейной теплопроводности

(5.23)

Ниже мы численно исследуем четыре примера, соответствующие двум различным выборам функции в первом случае является константой,

а во втором – линейной функцией времени:

(5.24)

(5.25)

Из (5.23) и (5.24) ясно, что с учетом соотношения (5.8) является соответственно линейной или квадратичной функцией времени. Мы рассматриваем начальные данные u0(x), совместные с асимптотическим условием (5.2), соответствующим, во первых, функции

(5.26)

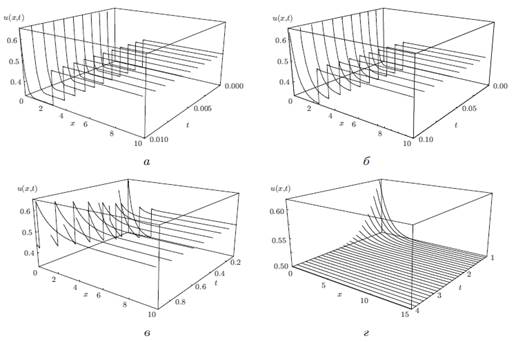
Рис. 5

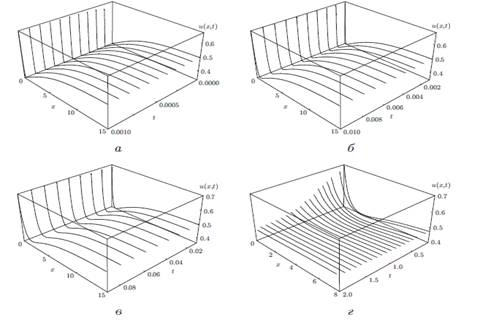
Графическое представление решения соответствующего примеру 5.2 построенное относительно переменной при фиксированных значениях для различных интервалов:

где – обычная единичная ступенчатая функция, а во-вторых, функции

(5.27)

где W(x) – W-функция Ламбера, неявно определяемая соотношением В первом случае с , определяющейся (5.23), наш метод состоит в прямом вычислении функции через явное решение, как это было показано в работе.Затем мы вычисляем функцию в соответствии с выражением (5.15) и окончательно получаем решение , обращая преобразование годографа (5.4)–(5.6). При фиксированном времени t = t* с помощью (5.4) и (5.5) получаем

(5.28)

Тогда из выражения (5.27) мы получаем обратную функцию и окончательно находим решение исходной задачи:

(5.29)

в соответствии с (5.4).

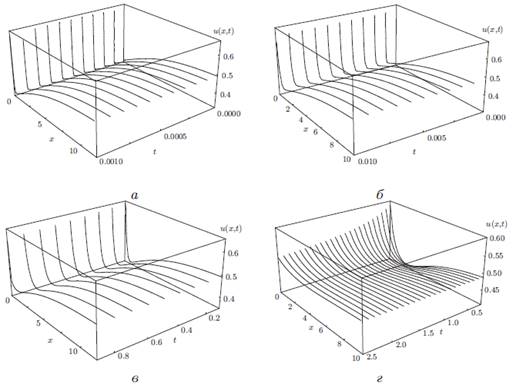
Рис. 6

Графическое представление решения соответствующего примеру 5.3 построенное относительно переменной при фиксированных значениях t для различных интервалов:

Если определяется (5.24), то интегральное уравнение Вольтерра (5.16) не решается в квадратурах, как в предыдущем случае, однако оно должно решаться численно. Решение линейной задачи получается с помощью уравнения (5.15), но, конечно, вычислительные издержки такого алгоритма гораздо больше, чем в предыдущем случае. Интегральное уравнение (5.15) интегрируется численно при использовании неравномерного fixed-mesh-метода, с тем чтобы избежать проблем, связанных с наличием умеренно сингулярного ядра. Как объяснялось выше, после вычисления функции мы, обращая преобразование годографа, получаем решение нелинейной задачи (см. (5.27)и (5.28)).

Ниже мы подробно анализируем примеры и интерпретируем численные результаты, представив ряд графиков. Подчеркнем, что на всех графиках каждая линия представляет собой функцию в фиксированный момент времени. Как и ожидалось, при больших x решение нелинейной задачи u(x, t) асимптотически приближается к значению .

Пример 5.1.

Функция u0(x) задается уравнением (5.25), а f(t) – уравнением (5.23),

где a=1 , Тогда

(5.1.1)