Курсовая работа: Теория распространения волн

4) работа сил трения;

5) внешняя механическая работа.

Учитывая допущения параграфа 2, четвёртый член обнуляется (отсутствие трения). Уравнение принимает вид:

(3.3)

Уравнение неразрывности запишется в виде:

,, (3.4)

где δσ – элемент поперечного сечение трубки тока в каком-либо месте, V_n - средняя скорость в

этом сечении, ρ=const - плотность жидкости (жидкость несжимаема – смотри §2).

Уравнения 3.1-3.4 являются исходными для проведения исследования. На них опираются все дальнейшие доказательства и выводы.

4. Преобразование исходной системы уравнений к расчётной форме.

4.1 Зависимость длины волны от скорости распространения. Механизмы возникновения волн на свободной поверхности жидкости.

Как было принято в пункте 2, движение частиц свободной поверхности в системе отсчёта, двигающейся с фазовой скоростью волны (с абсолютной скоростью движения гребней волн), происходит по траекториям, близким к окружностям. В указанной системе отсчёта движение является установившимся (см. рис. 4.1).

рис 4.1

????? ??????? ???????? ?, ?????? ??????????, ??????????? ???????? ????, ????????????? ?? ????????? ???????????, ????? r, ? ?????? ????????? ???? ??????? ?? ????? ?????????? ????? ?. ????? ? ??????????? ??????? ??????? ???????? ??????? ?? ??????? ???? ????? ?????

ω₁ = c - ;

а во впадинах волн

ω₂ = c + ;

Разность высот между наивысшим (h_в ) и наинизшим (h_н ) положениями точек свободной поверхности равна h = h_в - h_н = 2r.

После ряда допущений в уравнении 3.2 и интегрирования уравнения движения вдоль линии тока получается уравнение сохранения движения в одной из форм уравнения Бернулли. Далее представлен пошаговый вывод с постепенным введением допущений:

Уравнение 3.2 в проекциях на оси координат (при допущении, что среда идеальная и невязкая):

, ;

Этих двух уравнений достаточно для последующего вывода, в них проигнорирована одна из координат y – это допустимо, так как разговор идёт о двухмерном движении. Далее первое уравнение домножается на dx, второе домножается на dz и оба уравнения складываются:

Далее записывается уравнение линии тока (вторым допущением является то, что движение происходит только вдоль линии тока): , откуда . Это допущение позволяет группу слагаемых из левой части суммарного уравнения представить в виде

.

Действительно, .

Далее поле внешних сил принимается потенциальным (вообще говоря, в нашем случае это поле сил тяжести). Это означает, что существует такая силовая функция U, для которой и .

Тогда (первая скобка в правой части суммарного уравнения).

Последнее слагаемое суммарного уравнения есть не что иное, как - полный дифференциал давления P, делённый на плотность. Самая первая скобка суммарного уравнения в векторном виде запишется как . Теперь, когда все слагаемые рассмотрены, можно переписать суммарное уравнение в упрощённом виде: 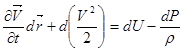. Дальнейшие упрощения приводят к обнулению первого члена этого уравнения, т. к. для установившегося течения . Теперь, ещё раз вспомнив о потенциальности поля сил тяжести, можно записать , .

Это значение подставляется в полученное дифференциальное уравнение, после чего последнее интегрируется вдоль линии тока:

,
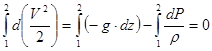