Действительно, . Поскольку , то, вставляя между g и f и используя ассоциативное свойство всякой композиции преобразований, получаем . Далее . Учитывая, что преобразование, обратное композиции данных преобразований, является композицией обратных им преобразований, взятых в обратном порядке, т.е. , получаем . Наконец, .

Если преобразование f инволютивно, то и то и f ^g также инволютивно. В самом деле, если , но f ≠ Е , то , но f ^g ≠ Е , так как из f ^g = Е следует f = Е .

Теорема о неподвижной точке. Если А – неподвижная точка преобразования f , то g ( A ) – неподвижная точка преобразования f ^g , и обратно:

f(A) = A ↔ f ^g (g(A)) = g(A).

Доказательство. Если f(A) = A, то f ^g (g(A)) = g(f(g^-1 (g(A)))) = =g(f(A)) = g(A) . Обратно, если f ^g (g(A)) = g(A) , т.е. g(f(g^-1 (g(A)))) = g(A), то g(f(A)) = g(A) . Поскольку при преобразовании образы любых двух различных точек не совпадают, то из совпадения образов точек f ( A ) и A при преобразовании g следует и совпадение этих точек: f ( A ) = A . [1]

Аналогичная теорема имеет место и для двойных прямых.

2. Трансформация движения движением

Применим теперь рассмотренные формулы и свойства к движениям. Если f и g – движения, то, в силу (1), f ^g – тоже движение. Более того, так как неподвижные точки движения f переходят в неподвижные точки движения f ^g , а вид движения характеризуется его неподвижными точками, то оба движения - f и f ^g – одного и того же вида, независимо от движения g .

2.1. Трансформация осевой симметрии движением

Принимая во внимание предыдущее свойство неподвижных точек и двойных прямых, получим

( S_l ) ^g = S_{g ( l )} . (3)

С помощью этой формулы можно получить аналогичные формулы для остальных движений частного вида. Для этого найдем сначала:

. [1]

2.2. Трансформация параллельного переноса движением

Если прямые u и v параллельны, то отображение g отображает их на параллельные прямые g(u) и g ( v ) с сохранением расстояния между ними. Следовательно, если , то

. (4)

В частности, если g есть поворот , то по свойству поворота ориентированный угол между векторами и равен углу α поворота. Отсюда из равенства следует, что результат поворота вектора не зависит от центра поворота.

Теорема. Для любого вектора , любого действительного числа х и перемещения g имеет место равенство:

. (5)

Доказательство. Если , то в силу (4) . Так как движение g сохраняет величину угла между векторами, а значит, и сохраняет, в частности, их сонаправленность или противонаправленность, то из или вытекает соответственно или . Отсюда и из равенства 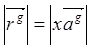следует (5).

Доказанная зависимость (5) с помощью первой формулы (2) обобщается на такую:

. (6)

Действительно, .

Ясно, что зависимость вида (6) будет справедлива и для линейной комбинации любого числа векторов. [1]

2.3. Трансформация поворота движением

Далее, если u ∩ v = O , то g ( u )∩ g ( v ) = g ( O ) и ( g ( u ), g ( v )) = ( u , v ) , если g – движение 1-го рода, и ( g ( u ), g ( v )) = -( u , v ) , если g – движение 2-го рода. Поэтому, если , то

(7)

где знак «+» берется при движении g 1-го рода и «-» - при движении g второго рода. [1]

В частности, если прямая l проходит через т.О пересечения прямых u и v , то

. (8)

2.4. Трансформация центральной симметрии движением

Так как центральная симметрия – частный случай поворота, а именно – поворот на 180°, то , а в силу формулы (7) , а это, в свою очередь, Z_{g ( O )} . Таким образом,

( Z_O ) ^g = Z_{g ( O )} . (9)

2.5. Трансформация зеркальной симметрии движением

Рассмотрим трансформацию преобразования пространства – зеркальной симметрии. Неподвижными точками преобразования являются точки g ( α ) , которые также образуют плоскость (по свойству движения), значит,

_. (10)

2.6. Трансформация поворота относительно оси движением

Поворот относительно оси l на угол α – это преобразование пространства, композиция двух зеркальных симметрий относительно плоскостей β и γ таких, что β∩γ = l , (β, γ) = α . Заметим, что в данном примере движение g также должно быть движением пространства, поэтому оно не может быть поворотом относительно точки. Далее, , по формулам (2) это равняется (по (10)). Пусть g (β)∩ g (γ) = m , ( g (β), g (γ)) = φ . Тогда по определению поворота относительно оси .