Курсовая работа: Цифровая фототриангуляция для создания топографических карт

геодезические координаты точек местности.

В начале известны координаты опорных точек в геодезической системе и фотограмметрические координаты этих точек, полученные из уравнивания сети. В качестве неизвестных выступают 7 элементов ориентирования геодезической сети:.

Определив 7 этих неизвестных, будут определяться геодезические координаты всех точек сети ПФТ.

6) исключение деформации сети.

Деформацию сети ПФТ можно описать различными полиномами.

Например, обобщённого типа:

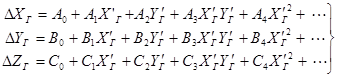, (1.10)

где– это коэффициенты деформации,– геодезические координаты точек сети, полученные на этапе 5 из геодезически ориентированной сети.

Из-за деформации сети после ее геодезического ориентирования на опорных точках будут получены расхождения координат :

(1.11)

Исключение деформации сети состоит из 2 процессов: сначала будут известны, опорных точек, неизвестными будут коэффициенты, а исходными для определения коэффициентов будут уравнения(1.10).

После определения коэффициентов деформации вычисляется величина разностикоординатхарактеризующие деформацию сети для всех точек сети по формулам (1.10).

Затем вычисляются исправленные координаты точек сети:

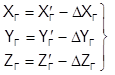. (1.12)

1.3.2 Построение блочных сетей фототриангуляции методом связок

Наиболее строгим методом построения блочных сетей пространственной фототриангуляции аналитическим и цифровым способами по сравнению с методом независимых моделей является метод связок[2]. В основе метода связок лежат уравнения коллинеарности проектирующих лучей:

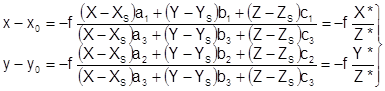, (1.13)

В уравнении будут известны f, x₀ , y₀ ,x, y. Неизвестны элементы внешнегоориентирования снимков, также X, Y, Z – координаты точек сети ПФТ.

Уравнения (1.13) нелинейные и решаются итерационным методом.

На основе (1.13) имеем уравнение поправок вида:

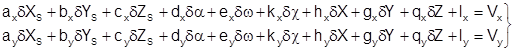, (1.14)

Уравнения (1.14) решаются по методу наименьших квадратов.

l_x и l_y – свободные члены, вычисляемые по формулам:

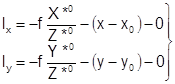, (1.15) где

– вычисляются по формулам (1.13) подстановкой в нихприближённых значений неизвестных.

Достоинством метода связок является то, что сеть строится и уравнивается одновременно для всех точек, входящих в блок, а также поправки находятся непосредственно к измеренным величинам, что обеспечивает более высокую точность построения сети. Недостатками этого метода являются: сложность задания приближённых значений неизвестных (для решения этой проблемы можно предварительно уровнять сеть менее строгим методом, а её результаты использовать в качестве приближённых значений), должны отсутствовать грубые ошибки, должны быть исключены систематические ошибки (или сведены к минимуму).

1.3.3 Построение блочной сети фототриангуляции объединением одиночных моделей

Этот метод основан на том[2], что сначала по каждой стереопаре, входящей в блок, строятся независимые одиночные модели, каждая из которых имеет свой масштаб и свою систему координат.

В процессе уравнивания моделей в блоке, все независимые модели приводятся к определенному масштабу и в единую пространственную систему координат на основе совместного внешнего ориентирования моделей.