Курсовая работа: Цифровая фототриангуляция для создания топографических карт

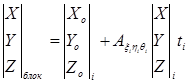, (1.16)

где i – номер модели,- элементы внешнего ориентирования для каждой модели. Исходными данными для формирования блока из независимых моделей служат, и. Используются условия равенства 0:

- разностейкоординат опорных точек, полученных из фототриангуляции и из полевых геодезических работ:

- уклоненийкоординат центров проектирования, полученных из ПФТ и зафиксированных в полете с помощью бортовых приборов;

- расхожденийкоординат связующих и общемаршрутных точек, лежащих в зоне поперечного перекрытия снимков соседних маршрутов.

Эти уравнения будут составляться для опорных точек и центров фотографирования.

Для связующих точек, расположенных в зоне тройного продольного перекрытия снимков и общемаршрутных точек, расположенных в зоне поперечного перекрытия снимков будут составляться уравнения вида:

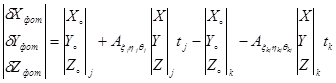(1.17)

Уравнения (1.16) и (1.17) решаются совместно. В результате решения определяются: , по которым далее по формулам (1.16) определяются координаты X, Y, Z в системе координат блочной сети.

Достоинством этого метода является то, что он проще в реализации, а недостатком – он менее строг с точки зрения уравнивания, чем метод связок.

1.3.4 Построение блочной сети фототриангуляции объединением независимых маршрутных моделей

Сущность данного метод заключается в том[2], что объединяются независимые маршрутные сети (построенные допустим методом независимых и частично зависимых моделей). Маршрутные сети предварительно внешне ориентированы в единой пространственной прямоугольной системе координат блока. В основе объединения маршрутных сетей в единый фототриангуляционный блок используется равенство нулю: 1) разности геодезических координат полученных из геодезии и ПФТ δгеод; 2) уклонений координат центров фотографирования, полученных из фототриангуляции и зафиксированных в полёте с помощью бортовых приборов δборт;

3) расхождений координат общемаршрутных точек δфот.

Исходными данными для объединения маршрутных сетей в единый блок служат, и .

Уравнивание маршрутных сетей в блоке выполняется одновременно с исключением деформации сетей ПФТ.

, (1.18)

где i – номер маршрутной модели,

C_i – коэффициенты, характеризующие деформацию фототриангуляционной маршрутной сети.

, (1.19)

где R_i – систематическая погрешность показаний бортовых навигационных приборов;

(1.20)

Уравнения (1.19) – (1.20) решаются совместно, из которых определяются неизвестные C_i и R_i .

На втором этапе для всех точек маршрутных сетей вычисляются велечины поправок

(1.21)

Вид функции (1.21) определяется типом выбранных для уравнивания полиномов .После вычисленияможно найти исправленные координаты точек сети:

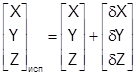(1.22)

Достоинством данного метода является то, что он проще в реализации, легче выявлять грубые ошибки в координатах общемаршрутных точек, а также результаты ПФТ по данному методу можно использовать в качестве приближённых значений неизвестных. Недостаток жёсткие требования к расположению опорных точек и их числу, также уравниваются функции от измеренных величин, а не сами измеряемые величины.

1.4 Особенности цифровой фототриангуляции

Пирамиды изображений для хранения цифровых изображений.