Курсовая работа: Цифровая фототриангуляция для создания топографических карт

К недостаткам алгоритма взаимной корреляции относятся:

- большой объем вычислений;

- алгоритм устойчиво работает только при следующих условиях: снимаемая местность плоская, взаимные углы наклона и разворота снимков не превышают 20-30°, а разномасштабность снимков менее 20-30%.

Метод наименьших квадратов

Для метода наименьших квадратов в качестве критерия подобия служит функция суммы квадратов разностей между яркостями пикселей двух изображений.

Пусть на ограниченном участке (x'[-M/2, M/2], y'[-N/2, N/2]) между функциямиf₁ и f₂ существует зависимость:

(1.24)

Для определения искомых величинp₀ иq₀ составим функцию:

(1.25)

Данную функцию решаем под условием минимума:

, (1.26)

Если известны приближенные значения неизвестных параметров (), то раскладывая функцию(1.25) в ряд Тейлора и ограничиваясь величинами первого порядка малости получаем линейное уравнение относительно неизвестных Dp₀ иDq₀ :

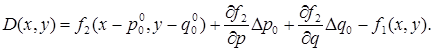(1.27)

В результате приходим к системе уравнений поправок:

(1.28)

гдеA– матрица коэффициентов уравнений поправок;

dX – вектор-столбец поправок к приближенным значениям неизвестных (Dp₀ и Dq₀ );

V – вектор невязок уравнений, который характеризует величины шумовых составляющих.

От системы уравнений поправок переходим к системе нормальных уравнений:

(1.29)

где и .

После определенияDp₀ иDq₀ уточняют значения искомых параметровp₀ иq₀ и затем выполняют следующую итерацию. Этот процесс повторяется до получения требуемой точности вычисления неизвестных.

Алгоритм наименьших квадратов по сравнению с методом взаимной корреляции обладает рядом следующих преимуществ.

Во-первых, метод наименьших квадратов позволяет оценить точность определения искомых параметров. Для оценки точности используют среднюю квадратическую ошибку (СКО) единицы веса, которая будет характеризовать влияние шумовых составляющих и качество образца, и СКО определения параметров p₀ и q₀ , характеризующие точность отождествления соответственно по осям x и y. Значение СКО единицы веса определяется по известной формуле:

(1.30)

где n – количество уравнений поправок, а k – количество неизвестных.

СКО определения неизвестных p₀ и q₀ выражаются формулами:

(1.31)

где и – соответствующие диагональные элементы обратной матрицы нормальных уравнений.

Во-вторых, метод наименьших квадратов позволяет вести не глобальный поиск соответственной точки, подставляя все возможные значения p и q, как в методе взаимной корреляции, а вдоль направления градиента функции.