Курсовая работа: Цифровая система передачи непрерывных сообщений

Подлежат расчету:

- энтропия квантованных отсчетов ;

- скорость создания информации на выходе АЦП .

Квантованный сигнал является дискретным по уровню и его энтропия вычисляется по формуле

, (3.7)

(полагают, что производимые в АЦП отсчеты независимы). Входящие в эту формулу вероятности квантованных значений сигнала можно определить

, (3.8)

где - квантованное значение сигнала на i-ом уровне квантования;

- плотность вероятности сигнала ;

- шаг квантования, определяемый по формуле (2.11).

Расчеты энтропии квантованного сигнала выполним с помощью ЭВМ.

Для ДЭР

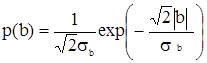(3.9)

Некоторые источники передают сообщения с фиксированной скоростью, затрачивая в среднем время Т на каждое сообщение. Производительностью (в бит на секунду) такого источника H'(B) называется суммарная энтропия сообщений, переданных за единицу времени:

(3.10)

.

Разницу между полученными значениями и ( < ) можно объяснить тем, что код на выходе АЦП обладает некоторой избыточностью. Эта избыточность связана с применением двоичного кода, из-за которого число уровней квантования сигнала определяется формулой и превышает необходимое а также, тем , что любой кодер должен обладать большей производительностью чем источник сообщения, что бы успевать его обрабатывать.

4. РАСЧЕТ ПОМЕХОУСТОЙЧИВОСТИ ДЕМОДУЛЯТОРА ДИСКРЕТНОЙ МОДУЛЯЦИИ

Требуется рассчитать:

- зависимость вероятности ошибки бита от отношения сигнал/шум на входе демодулятора и построить график этой зависимости;

- значения требуемых отношений сигнал/шум на входе демодулятора и , обеспечивающих допустимую вероятность ошибки бита .

Помехоустойчивость демодулятора сигнала дискретной модуляции определяют вероятностью ошибки сигнала либо вероятностью ошибки двоичного символа р. Вероятности ошибки и р зависят от вида модуляции, способа приема, отношения энергии сигнала к удельной мощности помехи и характеристик канала связи.

Для двоичных сигналов и р совпадают. Формулы для расчета вероятности ошибки символа при передаче двоичных сигналов по гауссовскому каналу связи с постоянными параметрами приведены в [2, разд. 6.5, 6.6]. Для ОФМ-2 вероятность ошибки двоичного кода будет определяться по формуле:

(4.1)

где

- функция Крампа.

Для заданного вида модуляции и способа приема рассчитаем и построим график зависимости

(4.2)