Курсовая работа: Визначення динамічних похибок вимірювань

Перехідна функція

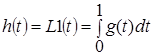. (2.6)

є відгуком динамічної системи на вхідну дію у вигляді одиничної функції , похідна якої

(2.7)

З характеристиками перетворення у часовій області однозначно пов’язані характеристики перетворення в частотній області, що є наслідком дуальності часу і частоти.

Усталена реакція на синусоїдний вхідний сигнал у загальному випадку є складною функцією параметрів засобу вимірювальної техніки і описується відповідними амплітудно-частотною та фазочастотною характеристиками, які можуть бути одержані з диференціального рівняння в результаті нижчеподаних математичних дій.

Застосувавши до диференціального рівняння при початкових нульових умовах перетворення Лапласа, одержимо передаточну функцію

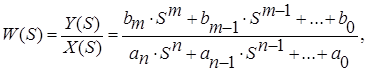(2.8)

де - оператор Лапласа, та - зображення за Лапласом відповідно вихідної та вхідної величин.

Заміна оператора Лапласа в передаточній функції на дає комплексну частотну характеристику

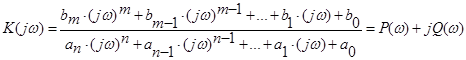(2.9)

Комплексна частотна характеристика є вихідною для визначення амплітудно-частотної

(2.10)

(2.11)

Згідно індивідуального завдання необхідно знайти розв’язок диференціального рівняння другого порядку

, (2.12)

. (2.13)

Підставимо (2.13) в (2.12) і отримаємо:

. (2.14)

Розв’язком даного рівняння буде функція

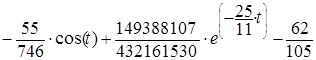, (2.15)

графічне зображення якої подано на рисунку 2.1.

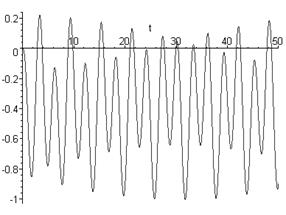
Рисунок 2.1 – Графічне представлення розв’язку диференціального рівняння

Для знаходження перехідної характеристики підставимо в (2.12) як вхідний сигнал :

. (2.16)

Отримаємо розв’язок: