Курсовая работа: Выбор и построение интерполирующей функции
Пусть дана f задана таблично в точках хi она принимает значения уi = f(хi ) (i=0,1,…,n). Требуется вычислить значение функции f в некоторой точке х![]() , не совпадающей с точками хi. В таком случае нет необходимости строить общее выражение многочленна Лагранжа явно, а требуется только вичислить его значение в точке х. Эти вычисления удобно выполнить по интерполяционной схеме Эйткина. Характерной чертой этой схемы является единообразие вичислений.
, не совпадающей с точками хi. В таком случае нет необходимости строить общее выражение многочленна Лагранжа явно, а требуется только вичислить его значение в точке х. Эти вычисления удобно выполнить по интерполяционной схеме Эйткина. Характерной чертой этой схемы является единообразие вичислений.
Если функция f задана в двух точках х0 и х1 значениями у0 и у1 , то для вычисления ее значения в точке х![]() можно воспользоваться формулой:
можно воспользоваться формулой:
 (*) линейного интерполирования.
(*) линейного интерполирования.
Обозначив значение функции в точке x через ![]() , формулу (*) можно представить в таком виде:
, формулу (*) можно представить в таком виде:
 ,
,
Где в правой части стоит определитель 2-го порядка. Эта формула эквивалентна формуле (*). Кроме того,  ,
, ![]() .
.
Пусть функция f задана в трех точках х0 , х1 и х2 своими значениями у0 , у1 и у2 и требуется вычислить ее значение в точке х![]() . В этом случае по схеме Эйткина в точке х вычисляют сначала значения двух линейных многочленов
. В этом случае по схеме Эйткина в точке х вычисляют сначала значения двух линейных многочленов
![]() и
и  ,
,
а затем значение квадратичного многочлена вида:
 .
.
Непосредственной подстановкой убеждаемся, что ![]() ,
,
![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
Покажем еще, что ![]() совпадает с формулой Лагранжа для трех узлов интерполирования. Поскольку
совпадает с формулой Лагранжа для трех узлов интерполирования. Поскольку
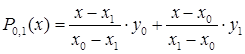
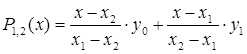 ,
,
то, раскрывая определитель, получаем:
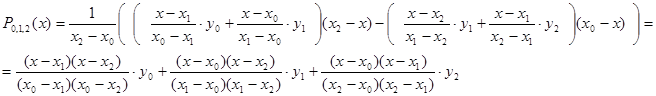
Эта схема обобщается на более высокие степени. Если функция f задана в четырех точках, то кубическое интерполирование выполняется по формуле
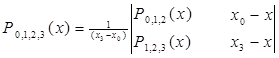 ,
,
Где ![]() и
и ![]() - значения квадратичных многочленов в точке х
- значения квадратичных многочленов в точке х![]() . Непосредственной проверкой убеждаемся, что
. Непосредственной проверкой убеждаемся, что ![]() и
и ![]() . Кроме того
. Кроме того ![]() совпадает с кубическим интерполяционным многочленом Лагранжа:
совпадает с кубическим интерполяционным многочленом Лагранжа:
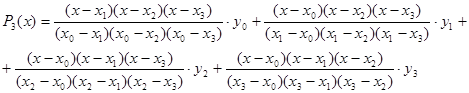 .
.
Вообще, если в (n+1)-й точке хi (i=0,1,…,n) функция f принимает значения yi (i=0,1,…,n), то значение интерполяционного многочлена Лагранжа степени n в точке х![]() можно вычислить по формуле
можно вычислить по формуле
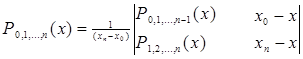 ,
,
где ![]() и
и ![]() - значения интерполяционных многочленов, вычисленных в точке х на предшествующем шаге. Ясно, что для вычисления значения многочлена степени n в точке х необходимо по схеме Эйткина вычислить в этой точке значения n линейных, n-1 квадратичных, n-2 кубических многочленов и т. д., два многочлена степени n-1 и, наконец, один многочлен степени n. Все эти многочлены выражаются через определитель 2-го порядка, что делает вычисления единообразными.
- значения интерполяционных многочленов, вычисленных в точке х на предшествующем шаге. Ясно, что для вычисления значения многочлена степени n в точке х необходимо по схеме Эйткина вычислить в этой точке значения n линейных, n-1 квадратичных, n-2 кубических многочленов и т. д., два многочлена степени n-1 и, наконец, один многочлен степени n. Все эти многочлены выражаются через определитель 2-го порядка, что делает вычисления единообразными.
Отметим то, что схема Эйткина применима и в случае неравноотстоящих узлов интерполирования.
Сплайн – интерполяция
В инженерной практике график функции y(xi ) (i=0,N) строят в основном с помощью лекал. Если точки размещены редко, то пользуются гибкой линейкой (spline), ставят ее на ребро и изгибают так, чтобы она одновременно проходила через все точки.
Поскольку приближенное уравнение изгиба пружинистого бруса имеет вид ![]() , то можно допустить, что ее форма между узлами есть алгебраический полином 3-й степени.
, то можно допустить, что ее форма между узлами есть алгебраический полином 3-й степени.
Вероятно, интерполирующую функцию между каждыми двумя узлами можно взять, например, в таком виде: