writeln;

end;

readkey;

DoneWinCrt;

end.

Входными данными для этой программы есть: количество узлов интерполирования и значения функции y_i , для которых надо построить конечные разности.

Решение в Excel

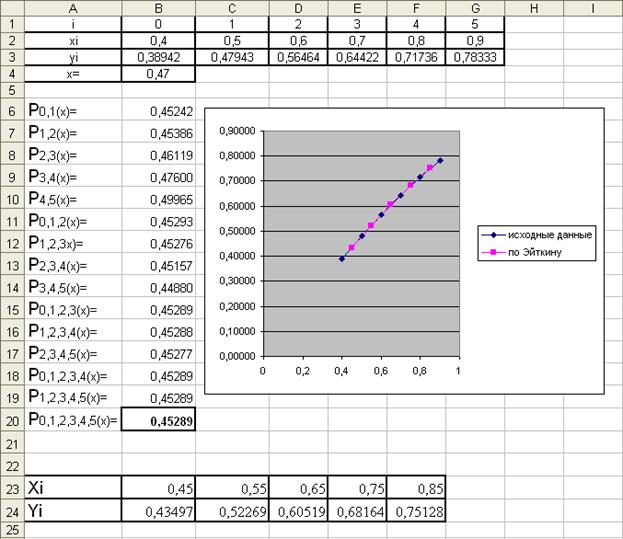
Для проверки вычислений я решил поставленную задачу в Excel по схеме Эйткина:

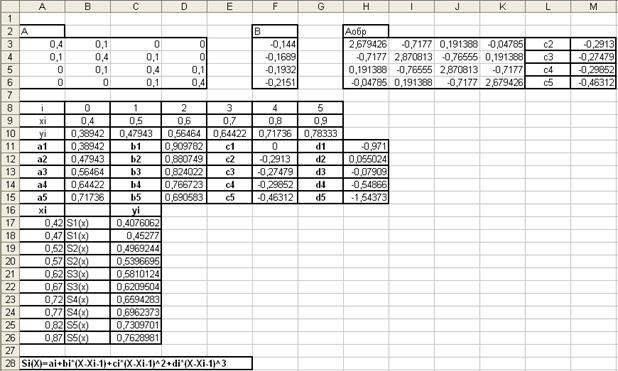
Также в целях проверки вычислений я решил данную задачу с помощью кубических сплайнов:

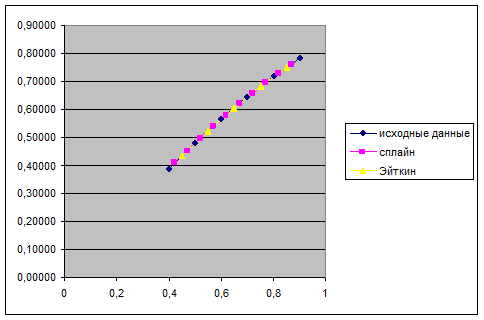
График, отображающий значения функции, вычисленные по схеме Эйткина и с помощью кубических сплайнов:

Выводы

Все многочлены, которые надо вичислить для данного х выражаются через определитель 2-го порядка, что делает вычисления единообразными. Схему Эйткина просто программировать.

Можно отметить то, что схема Эйткина применима и в случае неравноотстоящих узлов интерполирования, то есть ее можно применять для любого шага интерполирования. Также надо отметить то, что, если в задаче требуется вычислить значение функции в одной точке, нет необходимости строить общее выражение многочленна Лагранжа или Ньютона явно, а требуется только вичислить его значение в точке х. Эти вычисления удобно выполнить по интерполяционной схеме Эйткина.

Сопоставим исходные данные, у нас имеется 6 узлов интерполирования. По этим точкам можно построить интерполяционный полином, причем 5-й степени, привлекая к исследованию интерполяцию кубическим сплайном, утверждаю, что данным методом можно построить на каждом подинтервале полином 3-й степени. Последним словом в выборе между первым и вторым методом будут конечные разности на заданном множестве узлов. Конечные разности являются аналогом производной от функции. В данном случае конечные разности использованы для определения степени полинома и для определения полином данная функция или нет, с помощью которого можно максимально приблизить данную функцию.

Данного количества узлов интерполирования не достаточно для точного определения является ли данная функция полиномом, то есть в данном случае конечные разности не являются точным критерием для выбора между двумя методами интерполирования.

Эйткин
x=	0,47
y=	0,45289

сплайн
x=	0,47
y=	0,45277

В результате вычисления значения функции в точке 0,47 видно что значения функции в искомой точке мало отличимые. То есть в данном случае можно применять оба метода.

Если взять точность вычисления до четвертого знака после запятой, то степень полинома по данным конечных разностей будет полином 3-й степени. Поскольку по схеме Эйткина строятся все полиномы степени не выше 6-й. И в этом случае лучше применять кубические сплайны.

Список использованной литературы

1. Б. П. Демидович и И. А. Марон. “Основы вычислительной математики”, Москва, 1963г.

2. Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. “Численные методы”, Москва, 1987г.

3. Козин А. С., Лященко Н. Я. Вычислительная математика: Пособие для факультативных занятий в 10 классе.- К.: Рад. школа, 1983. – 191 с.

4. Мусіяка В. Г. Основи чисельних методів механіки: підручник. – К.: Вища освіта, 2004. – 240 с.: іл.

5. Л. Д. Назаренко Чисельні методи. Дистанційний курс.

Приложение

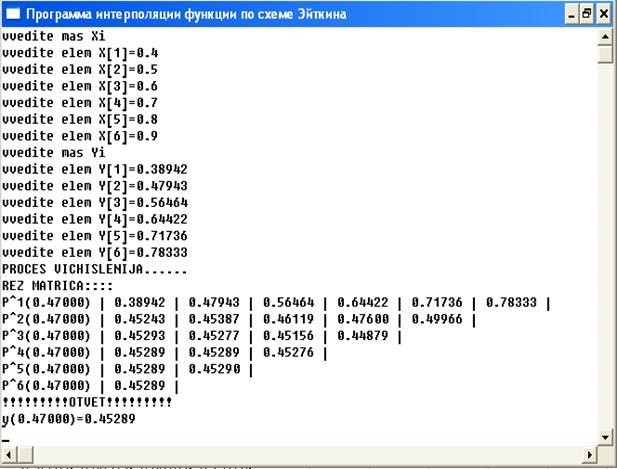
Результаты работы программы EITKIN:

Результаты работы программы konechn_razn: